Quad-Optimized Low-Discrepancy Sequences
DOI: https://doi.org/10.1145/3641519.3657431
SIGGRAPH Conference Papers '24: Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers '24, Denver, CO, USA, July 2024
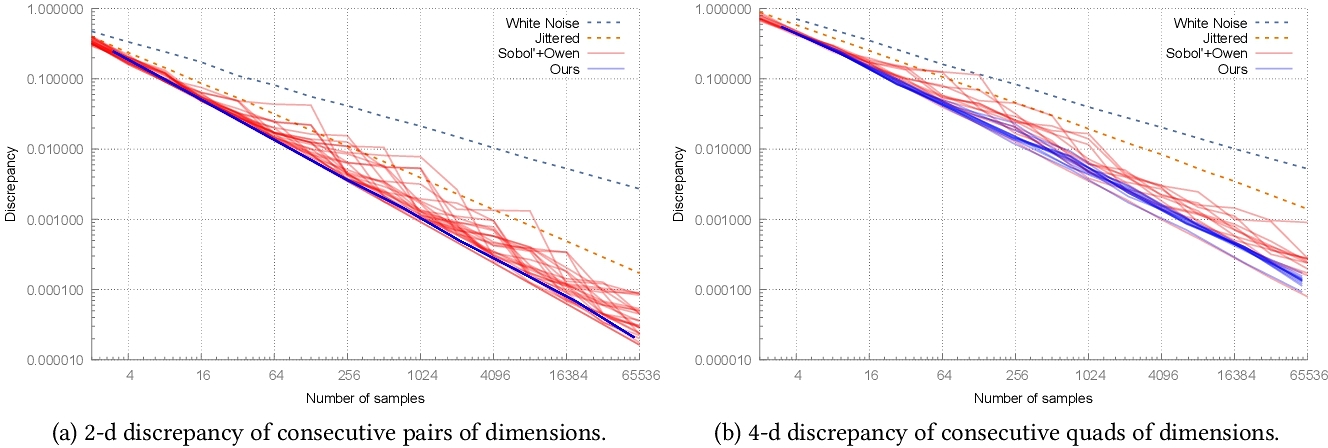
The convergence of Monte Carlo integration is given by the uniformity of samples as well as the regularity of the integrand. Despite much effort dedicated to producing excellent, extremely uniform, sampling patterns, the Sobol’ sampler remains unchallenged in production rendering systems. This is not only due to its reasonable quality, but also because it allows for integration in (almost) arbitrary dimension, with arbitrary sample count, while actually producing sequences thus allowing for progressive rendering, with fast sample generation and small memory footprint. We improve over Sobol’ sequences in terms of sample uniformity in consecutive 2-d and 4-d projections, while providing similar practical benefits – sequences, high dimensionality, speed and compactness. We base our contribution on a base-3 Sobol’ construction, involving a search over irreducible polynomials and generator matrices, that produce (1, 4)-sequences or (2,4)-sequences in all consecutive quadruplets of dimensions, and (0, 2)-sequence in all consecutive pairs of dimensions. We provide these polynomials and matrices that may be used as a replacement of Joe & Kuo's widely used ones, with computational overhead, for moderate-dimensional problems.
ACM Reference Format:
Victor Ostromoukhov, Nicolas Bonneel, David Coeurjolly, and Jean-Claude Iehl. 2024. Quad-Optimized Low-Discrepancy Sequences. In Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers '24 (SIGGRAPH Conference Papers '24), July 27--August 01, 2024, Denver, CO, USA. ACM, New York, NY, USA 9 Pages. https://doi.org/10.1145/3641519.3657431
1 INTRODUCTION
Integrating functions is at the core of many computer graphics – and other – systems. Perhaps the most common example in our community is the case of physically-based rendering, that involves integrating the rendering equation. This is most often performed through Monte Carlo integration, involving the evaluation of the integrand at random locations, or quasi-Monte Carlo integration, evaluating the integrand for pseudo-random well-located samples. Quasi-Monte Carlo integration benefits from Koksma-Hlawka's inequality: the convergence rate of the Monte Carlo integration estimator improves with the integrand regularity, and with samples uniformity. While the regularity of the integrand itself can be somewhat controlled via other variance reduction techniques, we focus on samples uniformity that does not require knowledge of the integrand. Over the years, much work has been devoted to producing extremely uniform samples that effectively improve Monte Carlo convergence rate, e.g., by optimizing samples according to various criteria. Still, Sobol’ sequences with Joe and Kuo initialization tables [Joe and Kuo 2008; Sobol’ 1967] and Owen scrambling [Owen 1995] remain used in many production rendering systems and simulators, despite suboptimal sample uniformity. This is due to many other advantages offered by this approach that are often overlooked by other researchers. First, Sobol's method produces a sequence of arbitrary length: this allows for progressively refining a rendering by adding samples while maintaining good Monte Carlo convergence. In many cases, competing methods only offer point sets that do not allow for progressive rendering, or provide sequences only up to a finite predetermined number of samples. Second, it works in (almost) arbitrary dimensions while many approaches remain low-dimensional or even 2-d. Third, samples are fast to generate, with a compact representation (a small binary matrix per dimension and low-order polynomial binary coefficients), while many other approaches require complex optimizations or storing the precomputed points themselves. Nevertheless, other production renderers may only use the first few dimensions of Sobol’ sequences due to their “increasingly poor distributions in pairs of higher dimensions” (regarding Renderman [Christensen et al. 2018]).
Based on this observation, we seek a way to improve Sobol’ samples uniformity on consecutive 2-d and 4-d projections while preserving their advantages. Sobol’ samples uniformity is guaranteed in part by construction, but also via appropriate parameter search. We leverage both aspects. First, we benefit from the additional degrees of freedom offered by a construction in base 3 rather than base 2 [Paulin et al. 2022]. Second, we benefit from other degrees of freedom offered by a search over irreducible polynomials instead of primitive polynomials [Faure and Lemieux 2016]. The relatively small number of irreducible polynomials still allows us for a comprehensive search, and allows us for finding solutions that provide the following desirable properties, that will be detailed in this paper. We show one quadruplet of dimensions (or quad hereafter, for short) that is a (1, 4)-sequence with (0, 2)-sequences pairwise projections, proven by construction. This provides ideal uniformity as measured in terms of discrepancy. We provide 11 additional quads of dimensions with the similar properties but only numerically verified up to nearly 59k samples. All quads we present are compatible: their dimensions do not overlap, and we use them together to form higher-dimensional sequences that posess (t, s)-sequence properties guaranteed by the Sobol’ construction, in up to 48 dimensions. We show that the discrepancy of our sequence is improved over Sobol’ on these consecutive projections. In exchange, a base-3 construction prevents the use of fast xor-based binary arithmetic, and can incur minor additional costs.
2 RELATED WORK
In its simplest form, quasi-Monte Carlo integration consists in numerically estimating an integral as
Much work has been devoted to improving the uniformity of generated point sets for improving the integration error.
Point sets.. Point sets have been numerically optimized specifically for improving uniformity. Optimal transport has been used as a measure of uniformity to minimize [De Goes et al. 2012] but this has remained limited to 2 or 3-dimensions. A sliced optimal transport variant allows to reach about 20 dimensions [Paulin et al. 2020; Salaün et al. 2022]. By instead optimizing the variance of the function obtained by summing Gaussians centered at each sample, Ahmed et al. [Ahmed et al. 2022] reach excellent uniformity, demonstrated up to 8 dimensions. Closer to our work, the cascaded construction of Paulin et al. [2021] based on alternating Sobol’ process with bit reversal, guarantees a perfect uniformity of the point set for projections onto consecutive pairs of dimensions in terms of discrepancy. The discrepancy of the first nested 100 dimensions is numerically optimized, although this does not guarantee a low discrepancy behavior (see next for a discussion on low-discrepancy sequences). All these approaches offer excellent uniformity, which translates into excellent numerical integration convergence, through Koksma-Hlavka's theorem but also other theorems bounding integration error with different kinds of discrepancy measures [Harman 2010], optimal transport metric [Paulin et al. 2020], or Fourier spectra behavior [Pilleboue et al. 2015]. Their main drawback is that they do not allow for progressive evaluation of the integral: once a numerical estimate has been obtained using a set of samples, refining this computation to improve its accuracy is not directly possible. This requires throwing away the previous result and producing a new completely different point set with more samples. Recently, Ahmed et al. [2023] introduced a method that allows converting certain point sets to sequences up to a finite predetermined number of samples. It is unfortunately limited to two dimensions, and using this process independently on different pairs of dimensions would deteriorate high-dimensional uniformity (as illustrated in Sec. 5 with ZeroTwo and Padded samplers). It is therefore not the solution we are looking for in higher dimensions.
Low-discrepancy sequences (LDS). Matrix-based constructions allow to produce sequences of points using finite field arithmetic. Among others, the Sobol’ sequence [Sobol’ 1967] has been most widely used. It produces points via modulo 2 matrix-vector multiplications, where the per-dimension binary triangular matrix is in part determined as a preprocess by optimizing generators (the first e × e upper left part of these matrices, where typically e ∈ [1, 18] depending on the dimension) and the rest of each matrix is obtained using a recursion involving a linear combination of previous columns weighted by the coefficients of a well-chosen primitive polynomial. While all these generators and primitive polynomials were carefully optimized, the obtained uniformity has remained limited (see Fig. 1 and 4) due to several constraints: the base 2 construction offers limited degrees of freedom and the set of primitive polynomials is small. However, they satisfy the important property of (t, s)-sequences, described hereafter. A point set of n = bm samples within the s-dimensional unit hypercube, where b is some base (b = 2 for Sobol), is said to be a (t, m, s)-net if all subintervals of volume bt/n of the form $\Pi _{j=1}^s [a_j b^{-d_j}, (a_j+1) b^{-d_j}]$ for all j contain bt samples, with $0\le a_j < b^{d_j}$, and $a_j, d_j \in \mathbb {N}_0$. Intuitively, t = 0 enforces high uniformity since it requires many small intervals each to contain a single point, while larger t values only enforce larger intervals to contain more points. A (t, s)-sequence is a sequence that enforces the (t, m, s)-net property for all possible values of m.
An advantage of (t, s)-sequence is that their discrepancy —and hence integration error— is bounded as a function of t [Niederreiter 1992] as:
(1)
In MatBuilder [Paulin et al. 2022], an integer linear program is designed to satisfy various user constraints on generative matrices. Contrary to Sobol’, these matrices are directly optimized, without resorting to polynomials, and they show that base-3 constructions offer significantly improved results due to the largely increased degrees of freedom. We take inspiration from this work to optimize Sobol’ generators in base b = 3. However, for a set of m × m optimized matrices, properties are only enforced up to bm samples. They hence cannot strictly produce “sequences” (where properties ought to hold for an arbitrary number of added points). We call these samplers “progressive” as in Ahmed et al. [2023]. In the work of Faure and Lemieux [2016], a Sobol’ construction based on irreducible polynomials instead of primitive polynomials is used for higher degrees of freedom. This construction has subsequently been used to numerically optimize generators in base 2 [Faure and Lemieux 2019]1. We also benefit from their result, seeking solutions for a subset of irreducible polynomials.
Other constructions have been proposed to produce low-discrepancy sequences, notably benefitting from the extremely high uniformity of low-dimensional Sobol’ sequences. The ZeroTwo approach presented in PBRT [Pharr et al. 2023] uses the first two dimensions of the Sobol’ sequence, and repeat them along with a random permutation of points to produce higher dimensional point sets. While pairing randomly loses the sequence property, shuffling indices instead with an Owen permutation allows to remain a sequence [Burley 2020; Helmer et al. 2021]. The first four dimensions can similarly be used [Burley 2020]. While these produce sequences with perfect projections on consecutive pairs of dimensions, their higher-dimensional behavior is not LDS anymore and loses benefits for general higher-dimensional integration problems [Helmer et al. 2021].
3 GENERALIZED SOBOL’ SEQUENCES
For completeness, this section describes the extension of Sobol’ sequences as described in the work of Faure and Lemieux [2016].
The construction is based on the following recipe. The general idea is to decompose the index of a point (say, point number i) in a chosen prime base b: ${\bf i}=(i_0, i_1,..., i_{m-1})_b = \sum _{k=0}^{m-1} i_kb^k$ and use this decomposition to produce point coordinates for each dimension. For a given dimension d, a matrix Cd with coefficients in {0,.., b − 1} is built such that the coordinate of that point for that dimension is obtained with the help of the matrix-vector multiplication j = CdiT. The d’th coordinate of point i is then expressed as xi, d = ∑kjkb− k − 1.
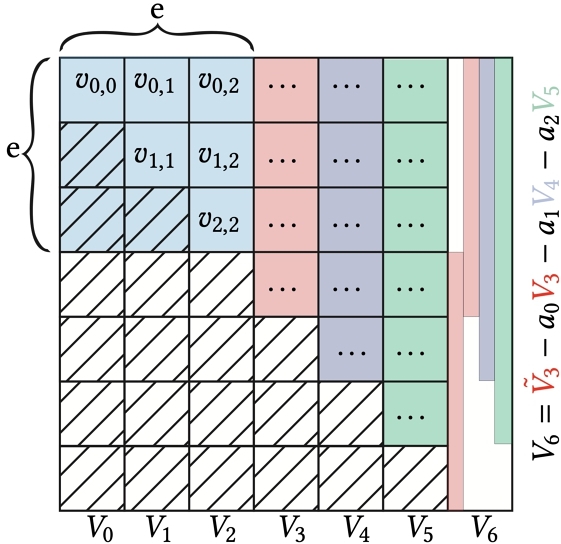
The power of Sobol’ construction lies in the way matrices Cd are obtained and the properties they guarantee on the generated points. Matrices Cd are upper triangular, with a non-zero diagonal. Its upper left ed × ed block consists of a set of ed · (ed − 1)/2 degrees of freedom ; these values are optimized in order to achieve good properties on the resulting points, as in the work of Joe and Kuo [Joe and Kuo 2008]. These first ed columns are called generating vectors. Typically, ed increases with the dimension d (e1 = 1 while e100 = 9 in the work of Joe and Kuo [Joe and Kuo 2008]).
Each column {Vn}n = e + 1..m of Cd is obtained as a linear combination of its ed previous columns, plus a shifted column (see Fig. 2). The coefficients in this combination are given by the coefficients of a polynomial $p_d(x) = \sum _{i=0}^{e_d} a_i x^i$ of degree ed:
(2)
While in the initial work of Sobol’ these polynomials were taken as primitive polynomials, Faure and Lemieux [2016] showed that similar guarantees were obtained using a larger set consisting of irreducible polynomials. Irreducible polynomials simply correspond to polynomials that cannot be divided by other polynomials other than themselves and 1 (similarly to prime numbers), while a primitive polynomial of degree m in base b carries the additional restriction that the smallest positive integer n such that it divides xn − 1 is n = bm − 1.
In particular, it is shown that for s matrices {C0,..., Cs − 1} obtained using irreducible polynomials of degrees {e0,..., es − 1}, the value for t is bounded by $t=\sum _{d=0}^{s-1} (e_d-1)$ [Faure and Lemieux 2016]. This in turn guarantees the low discrepancy of this sequence, though in practice, lower values of t may be found for specific generating vectors. This larger choice of polynomials (over primitive polynomials) allows to reduce the value of t because the degree of available polynomials grows much more gracefully. Similarly, the choice of a basis b = 3 is guided, in our work, by the added degrees of freedom hinted at by Paulin et al. [2022] as well as the slower growth of irreducible polynomials degree.
As an example, the first few primitive polynomials in base b = 3 are x + 1, x2 + x + 2, x2 + 2x + 2, x3 + 2x + 1, while the first few irreducible polynomials in base b = 3 are x, x + 1, x + 2, x2 + 1. Similarly, the first few irreducible polynomials in base b = 2 are x, x + 1, x2 + x + 1, x3 + x + 1. For primitive polynomials in base 3 and for irreducible polynomials in base 2, the fourth polynomial is already cubic while for base-3 irreducible polynomials it is only quadratic.
While in the case of b = 2, Joe and Kuo have extensively searched for good generating vectors with primitive polynomials [Joe and Kuo 2008] and Faure and Lemieux for irreducible polynomials [Faure and Lemieux 2019], such work has not been conducted for base 3 irreducible polynomials. The generating vectors we propose give desirable properties and benefit from Faure and Lemieux’ advances on Sobol’ sequences theory.
4 OPTIMIZING GENERATING VECTORS BASED ON QUADS
We first list the properties obtained by our sequences. The first 4 dimensions exhibit the following exceptional properties:
- (a) The first pair of dimensions (0, 1) is (0, 2)-progressive (up to m = 100)
- (b) The second pair (2, 3) is a (0, 2)-sequence (up to an infinite number of points)
- (c) Pairs (0, 2) and (0, 3) are (0, 2)-sequence (ditto)
- (d) Pairs (1, 2) and (1, 3) are (1, 2)-sequence (ditto)
- (e) The quad (0, 1, 2, 3) is a (1, 4)-sequence (ditto)
The other quads (4i, 4i + 1, 4i + 2, 4i + 3) exhibit the following good properties:
- (f) The first pair (4i, 4i + 1) is (0, 2)-progressive (up to m = 10, i.e., up to 310 ≈ 59k points)
- (g) The second pair (4i + 2, 4i + 3) is (0, 2)-progressive (ditto)
- (h) The quad (4i, 4i + 1, 4i + 2, 4i + 3) is at most (2, 4)-progressive (ditto)
The resulting sequence is a (t, s)-sequence, for some t, for any subset of dimensions – this is granted by design due to Sobol’ properties.
4.1 The first 4 dimensions
Low-dimensional problems are very common in practical applications, which justifies the search for exceptional properties. Fortunately, the availability of low-order irreducible base-3 polynomials allows us to exhibit such properties. For these first 4 dimensions, we use the first 4 irreducible polynomials in that order: $x, ~~x^2+1, ~~x+1, ~~x+2$. The four corresponding generating matrices are respectively [1], , [1], [2]. Reordering polynomials in this way allows for consecutive pairs of dimensions to remain (0, 2)-sequences. With these initializations, polynomial x generates the identity matrix, and x+1 generates the Pascal matrix modulo 3.
Properties (b), (c), (d) and (e) are immediately obtained by the theorem of Faure and Lemieux [2016] linking t with the sum of polynomial degrees (for any generating matrices). Property (e) should be compared to Sobol’ first four dimensions whose t value is t = 3 (with b = 2) while we obtain t = 1 (with b = 3). Property (a) has been numerically tested up to m = 100. We conjecture that it forms a (0,1)-sequence due to the self-similarity of the matrix involved, though we could not provide formal proof of that. For all practical purpose, the t value is 0 up to 3100 samples.
4.2 The other quadruplets
Contrary to the work of Faure and Lemieux [2019], we do not keep all irreducible polynomials to form higher dimensional problems, but we instead exhibit specific good irreducible polynomials with good generating matrices. Higher degrees irreducible polynomials make sequence properties harder to satisfy, so we numerically evaluate properties (f–h) only up to matrix sizes m = 10 (310 ≈ 59k points). The value of t for a given set of matrices {Ci}i = 1..k and given point set size bℓ can be computed as the value for which the matrix formed by combining the first ri rows and first ℓ columns of all matrices, with ∑iri = ℓ − t has (full) rank ℓ − t in GF(b), the Galois Field of order b [Niederreiter 1992; Paulin et al. 2023]. This is numerically tested for all ℓ ≤ m = 10, and we thus obtain a tℓ value – a t value per point set size.
We test all pairs of irreducible polynomials for up to the first 196 polynomials (of degrees 1 to 6), and for each pair, we test ∼ 10 million random generating vectors. We filter and select a subset of pairs that are (0, 2)-progressive, i.e., $t_\ell = 0 ~~\forall \ell \in \lbrace 1..m\rbrace$. We then exhaustively combine all pairs of generating vectors for dimensions of the form (i, j) for a given i against all other pairs of generating vectors for dimensions (k, l). For these quads (i, j, k, l), we only keep those whose maximum value of tℓ for all ℓ is at most equal to 2. When multiple solutions exist for the same quad, we finally keep the one for which this maximum value for t = 2 occurs for the largest value of ℓ. We remove all pairs involving dimension i and as well as the pair (k, l) from the list of pairs to evaluate, and iterate until no satisfactory quad is found.
This process allows to exhibit 11 quads of dimensions, that, when combined with the first excellent quadruplet, effectively produces progressive point sets of up to 48 dimensions.
5 NUMERICAL EXPERIMENTS
We analyze our sequences in terms of their 2-d projections, in terms of higher-dimensional discrepancies, integration error on synthetic integrands and integration error for rendering applications. Extensive experiments can be found in our supplementary document for all pairs and quads of dimensions.
5.1 Base-3 implementation
In our context, all arithmetic over GF(3) simply amounts to standard integer arithmetic modulo 3 (this is the case in GF(b) whenever b is prime, and as long as we do not require computing inverses). Base-2 arithmetic offers significant speed, due to bitwise operators. Notably a base-2 decomposition of a number can be obtained using bit shifts, and a modulo-2 bitwise addition amounts to a xor between two numbers. In contrast, a base-3 Sobol’ implementation requires decomposing a number in base 3, and performing matrix-vector multiplications and vector shifts, which reduces its efficiency. We rely on lookup tables to efficiently decompose in base 3 rather than slower successive divisions. A commonly used speedup in fast base-2 implementations relies on Gray-code ordering [Antonov and Saleev 1979]. We similarly benefit from this technique. Gray-code ordering allows to obtain a coordinate of the next sample point with a single column vector operation (instead of full matrix-vector product). The idea is that a single (base-3) digit is altered between two consecutive Gray-code indices, in such a way that, for a given dimension, a single column of our matrix affects the corresponding matrix-vector product.
For rendering applications, Owen scrambling allows to decorrelate sequences used in different pixels, and could be used to produce screen-space blue noise error distributions [Heitz and Belcour 2019]. Owen scrambling does not affect the value of t, and would not improve the uniformity of non-optimized projections (see Fig. 14 in supplementary materials). Base-3 Owen scrambling is required in our case, and is a trivial extension to base-2 Owen scrambling [Owen 1995] which proceeds by recursively swapping halves (and then quarters etc.) of each dimension. For each dimension separately, a ternary tree (instead of binary) is used to represent digit permutations. The root of the tree indicates whether the most significant digit of a point coordinate should be altered, and the leaves indicate whether the least significant digit should be altered. At each node of the tree, one permutation of the set {0, 1, 2} among b! = 6 pseudo-random permutations should be obtained or stored, and applied to the corresponding digit. We obtain this permutation by computing the tree's node index, and use it to index a random sequence. While similar in nature, the process in base 3 also incurs additional cost compared to base 2 scrambling due to the lack of bitwise operations.
We provide our base-3 implementations at https://github.com/liris-origami/Quad-Optimized-LDS, and pseudo-codes in a supplementary document.
5.2 2-d projections
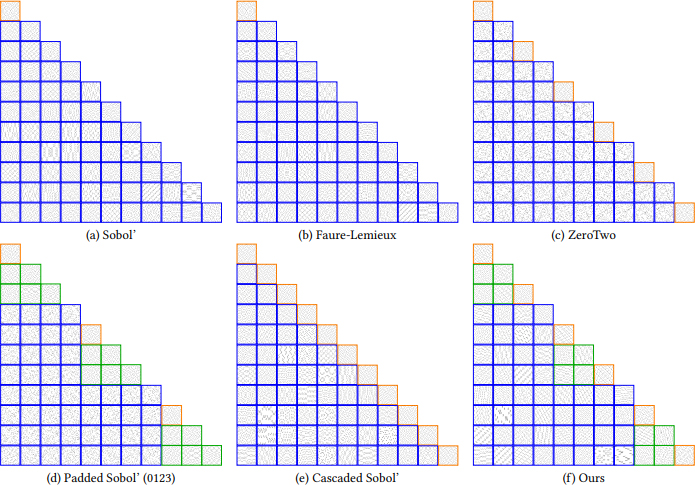
We illustrate the uniformity of our sequences in all pairs of projections in Fig. 4 as compared to Sobol, ZeroTwo (the first two dimensions of Sobol’ with random permutations), the ISN-dec LDS sequence optimized by Faure and Lemieux [2019], the first four projections of Sobol’ with random permutations as used by Burley [Burley 2020] for rendering, and the cascaded Sobol’ construction of Paulin et al. [Paulin et al. 2021]. The approach of Faure and Lemieux [2019] results in more uniform projections for distant pairs of dimensions while we improve uniformity on adjacent pairs of dimensions. Adjacent pairs of cascaded Sobol’ appear more uniform, but non-adjacent pairs are much less uniform. The ZeroTwo and Padded Sobol’ (0123) approaches result in white noise behavior for distant pairs of dimensions. Note that while we illustrate 2-d projections for 243 (resp. 256 in base 2) samples, behavior may change for other sample counts. We guarantee t = 0 for consecutive 2-d projections and t = 1 or t = 2 for consecutive 4-d projections at least for all sample counts until m = 59, 049, but t = 0 may be occasionally achieved by our sampler and others as well for a given sample count and pair of dimension. Also, t = 0 in base 2 involves a better uniformity than t = 0 in base 3, as discrepancy generally grows with b (Eq. 1). While some pairs of non-optimized projections appear very non-uniform (e.g., dimensions (7,11)), their 2-d discrepancy remains counterintuitively lower than that of white noise (see Fig. 5 in supplementary materials). If such structures need to be avoided, ZeroTwo or Padded Sobol’ remain good candidates in consecutive 2-d or 4-d projections but at the cost of lower convergence rate (see Sec. 5.3).
We evaluate the 2-d discrepancy and integration error for Gaussian and Heaviside integrands of 2-d consecutive projections as the number of samples increases. Fig. 3 (top) shows this data for two pairs, while graphs for all consecutive pairs are shown in supplementary materials. The supplementary materials also showcase an example of discrepancy above 310 samples (up to 531k samples), and for sample counts different from powers of 3. Cascaded Sobol’ [Paulin et al. 2021] offers best uniformity on consecutive 2-d projections as (0,2)-net property is enforced by construction, though their method does not result in a sequence. Aside from cascaded Sobol’, as dimensionality increases, our approach offers better uniformity and integration error over competitors, including Faure and Lemieux [2019]. Fig. 1 (a) summarizes all 2-d discrepancy curves on the same graph for our approach and Sobol’ for comparison.
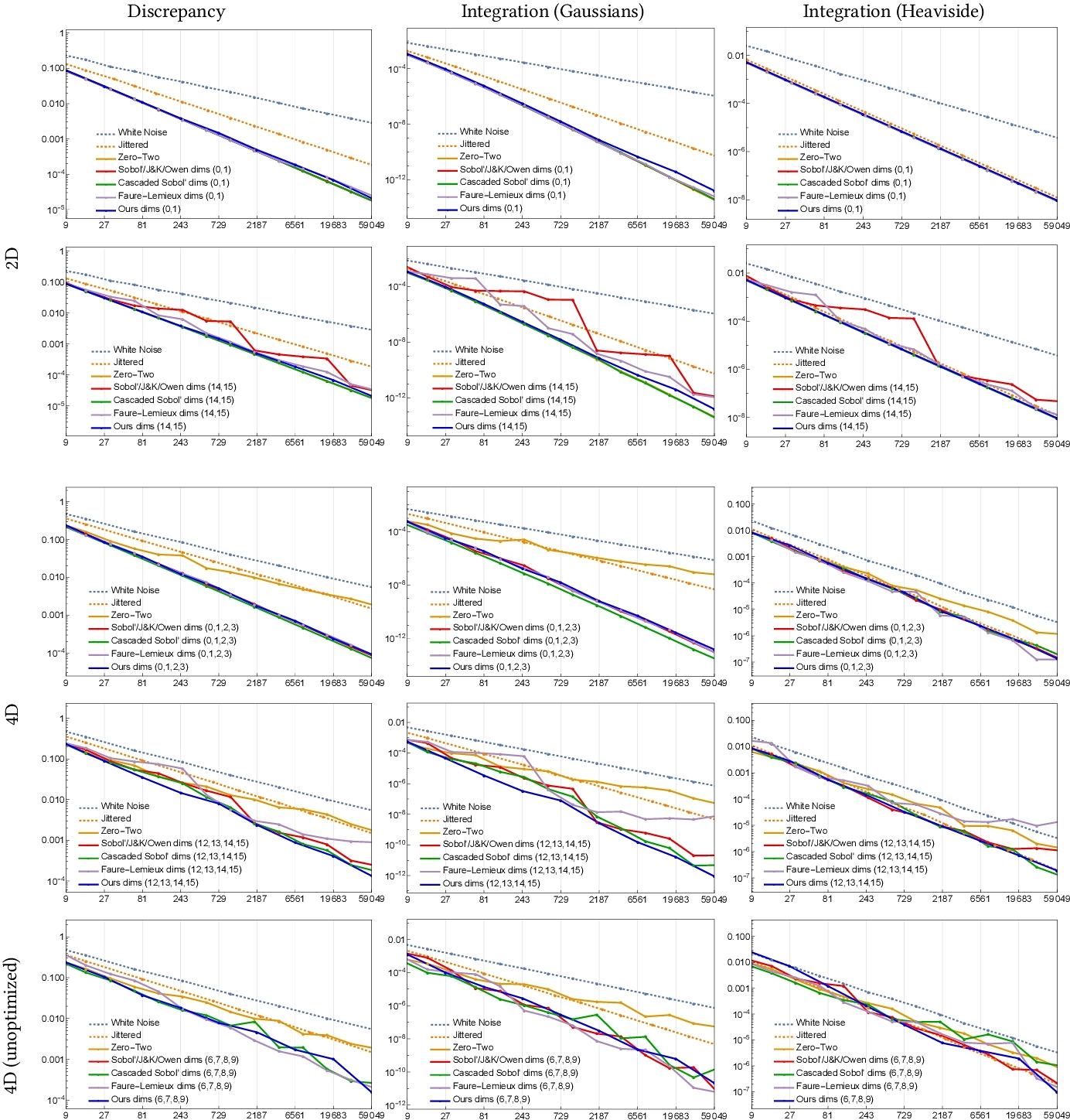
5.3 4-d and higher-dimensional discrepancies
As our approach is based on 4-d quads, we similarly evaluate the discrepancy behavior and integration error for consecutive quads. This is shown in Fig. 3 (bottom) for selected two quads, and all quads are shown exhaustively in supplementary materials with comparisons. Fig. 1 (b) summarizes all 4-d discrepancy curves on the same graph for our approach and Sobol’ for comparison.
In supplementary materials, we illustrate 6-, 8- and 12-dimensional discrepancies in Fig. 7, 8 and 9. Zero-Two and Padded Sobol’ have the same slope as white noise sampling due to the random pairing of blocks of dimensions.
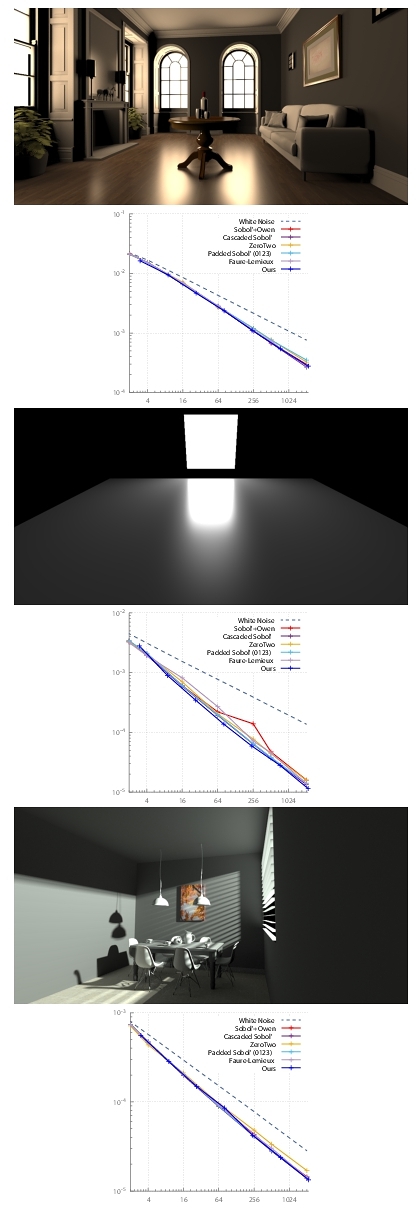
5.4 Rendering
We performed rendering experiments, in 6-d and 10-d. In the first experiments shown in Fig. 5 (top two rows), the scenes only have direct illumination. The first two dimensions are used for sampling light sources and the next two dimensions for sampling the BRDF ; a multi-sample MIS estimation is used to combine these estimators. The next two dimensions are used to sample within each pixel. The second experiment, shown in Fig. 5 (bottom row), adds one bounce of indirect lighting, involving 4 additional dimensions. Here, the first two dimensions are used for sampling within pixels, the next two dimensions for sampling light sources, the next two dimensions for sampling the BRDF (used both for MIS estimation of direct lighting like in the 6-d case, and for generating an indirect ray if the direct ray did not find a light source), the next four dimensions are used similarly at the next light bounce (sampling light sources and BRDF). In practice, dimension order did not significantly affect results. For direct light only, we improve the rendering error over other state-of-the-art samplers [Burley 2020; Faure and Lemieux 2019; Paulin et al. 2021; Pharr et al. 2023; Sobol’ 1967] on the simpler scene (middle row), while in the more complex scene (top row), Sobol’ with Owen scrambling, Faure and Lemieux’ and cascaded Sobol’ perform similarly to our method. In the case of indirect light (bottom row), we perform better than ZeroTwo [Pharr et al. 2023] that involves the first two Sobol’ dimensions, and similarly to the approach of Burley [2020] that involves the first four Sobol’ dimensions (padded Sobol’ (0123)). This underlines the importance of uniformity on consecutive quads. Neither the padded Sobol’ of Burley [2020] nor cascaded Sobol’ [Paulin et al. 2021] guarantee higher dimensional uniformity, although they work remarkably well on this example.
6 DISCUSSIONS AND CONCLUSION
We provide evidence for the existence of (0,2)-progressive pairs of dimensions in base b = 3 when using irreducible polynomials in Sobol’ construction [Faure and Lemieux 2016], that can be combined to form (2,4)-progressive quads. These quads allow for reducing the discrepancy in higher-dimensional problems and effectively reduce integration errors. We provide initialization tables in supplementary materials for moderate dimensions only (48 dimensions, as compared to the 10k dimensions of Joe & Kuo [2008] or 16,510 in the work of Faure and Lemieux [2019]). This limitation is not fundamentally linked to our approach, but by computer power and fine optimization of our unoptimized search implementation. The base-3 construction requires a base-3 Owen scrambling for rendering applications as well as modulo 3 arithmetic, which reduce speed compared to efficient bitwise operations. It also implies that sample counts of highest quality correspond to powers of 3, which grows faster than more commonly used powers of 2. Finally, aside from the first four dimensions, the only other criteria we enforced concerned sample sizes of up to nearly 59k samples. While we do not guarantee the best possible behavior for more than 59,049 samples and outside of the quadruplets of dimensions we optimized, a reasonable uniformity is guaranteed due to Sobol’ construction that enforces the (t, s)-sequence property and Faure and Lemieux's result bounding t by a sum of polynomial degrees [Faure and Lemieux 2016].
Within the context of moderate-dimensional problems where high uniformity in specific pairs of dimensions is desired, such as expected from rendering applications, our sampler should provide benefits for reducing integration error. We extensively tested our sampler based on a discrepancy metric and synthetic integrands, and offered preliminary experiments that exhibit such benefit in practice. We believe our sampler can spur further research in low discrepancy sampling.
ACKNOWLEDGMENTS
This work was partially funded by ANR-20-CE45-0025 (MoCaMed) and donations from Adobe Inc. We gratefully thank Christiane Lemieux (University of Waterloo) for providing us the code of Faure and Lemieux [2019].
REFERENCES
- Abdalla GM Ahmed, Jing Ren, and Peter Wonka. 2022. Gaussian blue noise. ACM Transactions on Graphics (TOG) 41, 6 (2022), 1–15.
- Abdalla GM Ahmed, Mikhail Skopenkov, Markus Hadwiger, and Peter Wonka. 2023. Analysis and synthesis of digital dyadic sequences. ACM Transactions on Graphics (TOG) 42, 6 (2023), 1–17.
- Ilya A Antonov and VM Saleev. 1979. An economic method of computing LPτ -sequences. U. S. S. R. Comput. Math. and Math. Phys. 19, 1 (1979), 252–256.
- Brent Burley. 2020. Practical hash-based Owen scrambling. Journal of Computer Graphics Techniques (JCGT) 10, 4 (2020), 29.
- Per Christensen, Julian Fong, Jonathan Shade, Wayne Wooten, Brenden Schubert, Andrew Kensler, Stephen Friedman, Charlie Kilpatrick, Cliff Ramshaw, Marc Bannister, et al. 2018. Renderman: An advanced path-tracing architecture for movie rendering. ACM Transactions on Graphics (TOG) 37, 3 (2018), 1–21.
- Fernando De Goes, Katherine Breeden, Victor Ostromoukhov, and Mathieu Desbrun. 2012. Blue noise through optimal transport. ACM Transactions on Graphics (TOG) 31, 6 (2012), 1–11.
- Henri Faure and Christiane Lemieux. 2016. Irreducible Sobol'sequences in prime power bases. Acta Arithmetica 173, 1 (2016), 59–80.
- Henri Faure and Christiane Lemieux. 2019. Implementation of irreducible Sobol'sequences in prime power bases. Mathematics and Computers in Simulation 161 (2019), 13–22.
- Glyn Harman. 2010. Variations on the Koksma-Hlawka inequality. Unif. Distrib. Theory 5, 1 (2010), 65–78.
- Eric Heitz and Laurent Belcour. 2019. Distributing Monte Carlo errors as a blue noise in screen space by permuting pixel seeds between frames. In Computer Graphics Forum, Vol. 38. Wiley Online Library, 149–158.
- Andrew Helmer, Per H Christensen, and Andrew Kensler. 2021. Stochastic Generation of (t, s) Sample Sequences. In EGSR (DL). 21–33.
- Stephen Joe and Frances Y Kuo. 2008. Constructing Sobol sequences with better two-dimensional projections. SIAM Journal on Scientific Computing 30, 5 (2008), 2635–2654.
- Harald Niederreiter. 1992. Random number generation and quasi-Monte Carlo methods. SIAM.
- Art B Owen. 1995. Randomly permuted (t, m, s)-nets and (t, s)-sequences. In Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing: Proceedings of a conference at the University of Nevada, Las Vegas, Nevada, USA, June 23–25, 1994. Springer, 299–317.
- Loïs Paulin, Nicolas Bonneel, David Coeurjolly, Jean-Claude Iehl, Alex Keller, and Victor Ostromoukhov. 2022. MatBuilder: Mastering Sampling Uniformity Over Projections. ACM Transactions on Graphics (SIGGRAPH) 41, 4 (Aug 2022).
- Lois Paulin, Nicolas Bonneel, David Coeurjolly, Jean-Claude Iehl, Antoine Webanck, Mathieu Desbrun, and Victor Ostromoukhov. 2020. Sliced optimal transport sampling.ACM Trans. Graph. 39, 4 (2020), 99.
- Loïs Paulin, David Coeurjolly, Nicolas Bonneel, Jean-Claude Iehl, Victor Ostromoukhov, and Alex Keller. 2023. Generator Matrices by Solving Integer Linear Programs. Technical Report arXiv:2302.13943.
- Loïs Paulin, David Coeurjolly, Jean-Claude Iehl, Nicolas Bonneel, Alexander Keller, and Victor Ostromoukhov. 2021. Cascaded Sobol'Sampling. ACM Transactions on Graphics (TOG) 40, 6 (2021), 1–13.
- Matt Pharr, Wenzel Jakob, and Greg Humphreys. 2023. Physically based rendering: From theory to implementation. MIT Press.
- Adrien Pilleboue, Gurprit Singh, David Coeurjolly, Michael Kazhdan, and Victor Ostromoukhov. 2015. Variance analysis for Monte Carlo integration. ACM Transactions on Graphics (TOG) 34, 4 (2015), 1–14.
- Corentin Salaün, Iliyan Georgiev, Hans-Peter Seidel, and Gurprit Singh. 2022. Scalable multi-class sampling via filtered sliced optimal transport. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia) 41, 6 (2022). https://doi.org/10.1145/3550454.3555484
- Il'ya Meerovich Sobol’. 1967. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel'noi Matematiki i Matematicheskoi Fiziki 7, 4 (1967), 784–802.
FOOTNOTE
1At the time of writing the result of this optimization is not publicly available. The authors have graciously provided us with six generators. We selected the best of these generators according to our criteria for comparison purposes
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for components of this work owned by others than the author(s) must be honored. Abstracting with credit is permitted. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee. Request permissions from permissions@acm.org.
SIGGRAPH Conference Papers '24, July 27–August 01, 2024, Denver, CO, USA
© 2024 Copyright held by the owner/author(s). Publication rights licensed to ACM.
ACM ISBN 979-8-4007-0525-0/24/07.
DOI: https://doi.org/10.1145/3641519.3657431