Neural Reasoning for Robust Instance Retrieval in SHOIQ
DOI: https://doi.org/10.1145/3731443.3771348
K-CAP '25: Knowledge Capture Conference 2025, Dayton, OH, USA, December 2025
Concept learning exploits background knowledge in the form of description logic axioms to learn explainable classification models from knowledge bases. Despite recent breakthroughs in neuro-symbolic concept learning, most approaches still cannot be deployed on real-world knowledge bases. This is due to their use of description logic reasoners, which are not robust against inconsistencies nor erroneous data. We address this challenge by presenting a novel neural reasoner dubbed Ebr. Our reasoner relies on embeddings to approximate the results of a symbolic reasoner. We show that Ebr solely requires retrieving instances for atomic concepts and existential restrictions to retrieve or approximate the set of instances of any concept in the description logic $\mathcal {SHOIQ}$. In our experiments, we compare Ebr with state-of-the-art reasoners. Our results suggest that Ebr is robust against missing and erroneous data in contrast to existing reasoners.
ACM Reference Format:
Louis Mozart Kamdem Teyou, Luke Friedrichs, N'Dah Jean Kouagou, Caglar Demir, Yasir Mahmood, Stefan Heindorf, and Axel-Cyrille Ngonga Ngomo. 2025. Neural Reasoning for Robust Instance Retrieval in SHOIQ. In Knowledge Capture Conference 2025 (K-CAP '25), December 10--12, 2025, Dayton, OH, USA. ACM, New York, NY, USA 8 Pages. https://doi.org/10.1145/3731443.3771348
Instance retrieval, Neural reasoner, Symbolic reasoner, Description logic, Concept learning, Knowledge base
1 Introduction
Description Logics (DLs) [1] offer a formal framework for structured knowledge representation and reasoning. Due to their well-defined semantics and favorable computational properties, DLs are now essential in fields such as ontology engineering [21], knowledge representation [5], and the Semantic Web [19]. Concept learning over DL Knowledge Bases (KBs) is a form of ante-hoc explainable supervised machine learning that returns a DL concept as a classifier.
Currently, concept learners rely on symbolic reasoners (e.g., Pellet [30], Fact++ [33] and HermiT [15] for instance retrieval. Although such reasoners are being successfully applied to infer concept hierarchies in ontological data [28, 35], their application on real data is limited by their inability to handle inconsistencies and to infer missing instance assertions. An inconsistency occurs when a knowledge base entails a contradiction, that is, when some assertions cannot simultaneously be true given the ontology's axioms. For example, consider the inconsistent knowledge base $\mathcal {K}=(\lbrace C\sqsubseteq A, C\sqsubseteq B, A\sqcap B \sqsubseteq \bot \rbrace, \lbrace C(a)\rbrace)$. A classical symbolic reasoner cannot determine the class membership of the individual a since it is inferred to be in both A and B, which leads to an inconsistency with the axiom A⊓B⊑⊥. By contrast, an incomplete knowledge base lacks certain facts or assertions that are true in the domain but absent from the data. For instance, $\mathcal {K}^{\prime }=(\emptyset, \lbrace \texttt{Person}(Bob), \texttt{Person}(Paul), \texttt{Person}(Ani),\\ \texttt{knows}(Bob, Paul), \texttt{knows}(Ani, Joe)\rbrace),$ where class memberships are missing for some individuals, e.g., Joe. In $\mathcal {K}^{\prime }$, a symbolic reasoner cannot infer that Joe is an instance of $\texttt{Person}$.
Inconsistency and incompleteness are well-recognized challenges in practical knowledge base applications, as real-world KBs-particularly large, evolving, or automatically constructed ones are rarely complete or fully consistent [24]. The presence of such imperfections is not only common but also well-documented; for instance, the DBpedia1 ontology contains conflicting assertions such as listing both $\texttt{Virginia}$ and $\texttt{British America}$ as George Washington's birthplace, despite their historical overlap. While standard DL reasoners are capable of detecting inconsistencies, they do not operate reliably in their presence, often halting entirely when even a few conflicting assertions exist in otherwise valid KBs. Our work builds on this motivation by introducing a novel application of knowledge graph embedding models for reasoning under inconsistency and incompleteness, offering a data-driven alternative to symbolic reasoning in settings where classical approaches break down.
With this work, we aim to further the development of scalable and robust concept retrieval by presenting a neural reasoner dubbed Ebr (Embedding Based Reasoner) that is robust against inconsistencies and missing assertions. Neural link predictors have been extensively investigated to deal with incompleteness on various datasets [14, 26]. Recent works showed that neural link predictors can be effectively applied to answer complex queries involving multi-model reasoning [2, 13]. Our approach Ebr leverages knowledge graph embeddings to perform robust instance retrieval over incomplete and inconsistent KBs. It relies on a simple neural link predictor to implement the robust retrieval of assertions from incomplete and inconsistent data. These assertions are combined via set-theoretic operations to compute instances of concepts. A summary of our contributions is as follows:
- We propose Ebr, a neural semantics that leverages knowledge graph embeddings to perform concept learning and instance retrieval over expressive KBs formulated in $\mathcal {SHOIQ}$, thereby extending the use of embedding models beyond traditional link prediction tasks.
- We provide an in-depth comparison of Ebr against symbolic reasoners on six datasets. We show that our approach outperforms symbolic methods on knowledge bases with a varying percentage of false or missing assertions.
- The source code of Ebr, along with the datasets and scripts used to reproduce these experiments, is publicly available2 to support further development.
2 Background and Related Works
2.1 Knowledge Bases in Description Logics
A knowledge base (KB) is a pair $\mathcal {K} = \langle \mathcal {T}, \mathcal {A}\rangle$. The TBox $\mathcal {T}$ contains general concept inclusions (GCIs) of the form C⊑D, where C, D are concepts. The ABox $\mathcal {A}$ includes assertions having the form C(a) (concept assertion) or r(a, b) (role assertion) for individuals a, b, concepts C, and role r. The description logic $\mathcal {SHOIQ}$ additionally includes an RBox, which contains axioms pertaining to roles. A role inclusion axiom (RIA) has the form r⊑s. A transitivity axiom is denoted by Tra(r), and a functionality axiom by Fun(r), where r and s are roles. A role s is simple if there is neither a transitivity axiom Tra(r), nor Tra(r− 1) for any role r subsumed by s. For simplicity of presentation, we assume that the TBox $\mathcal {T}$ includes both concept and role axioms. The syntax and semantics for concepts in $\mathcal {SHOIQ}$ [1, 18] are given in Table 1.
| Construct | Syntax | Semantics |
|---|---|---|
| Atomic concept | A | $A^{\mathcal {I}}\subseteq {\Delta ^\mathcal {I}}$ |
| Atomic role | r | $r^\mathcal {I}\subseteq {\Delta ^\mathcal {I}\times \Delta ^\mathcal {I}}$ |
| Top concept | ⊤ | $\Delta ^\mathcal {I}$ |
| Bottom concept | ⊥ | ∅ |
| Negation | ¬C | $\Delta ^\mathcal {I}\setminus C^\mathcal {I}$ |
| Conjunction | C⊓D | $C^\mathcal {I}\cap D^\mathcal {I}$ |
| Disjunction | C⊔D | $C^\mathcal {I}\cup D^\mathcal {I}$ |
| Existential restriction | ∃ r.C | $\lbrace x \mid \exists \ y. (x,y) \in r^\mathcal {I} \wedge y \in C^\mathcal {I}\rbrace$ |
| Inverse Role | r− 1 | $\lbrace (y,x) \mid (x,y)\in r^\mathcal {I}\rbrace$ |
| Nominals | {o} | $\lbrace o\rbrace ^{\mathcal {I}}\subseteq \Delta ^{\mathcal {I}}$ |
| At least restriction | ≥ ns.C | $\lbrace a \mid \; | \lbrace b\in C | (a,b) \in s^\mathcal {I} \rbrace | \ge n \rbrace$ |
| At most restriction | ≤ ns.C | $\lbrace a \mid \; | \lbrace b\in C| (a,b) \in s^\mathcal {I} \rbrace | \le n \rbrace$ |
Let C⊑D be a GCI and $\mathcal {I}$ be an interpretation. Then, $\mathcal {I}$ satisfies C⊑D, denoted as $\mathcal {I}\models {C}\sqsubseteq D$ iff ${C}^\mathcal {I}\subseteq {D}^\mathcal {I}$. Similarly, $\mathcal {I}$ satisfies an assertion C(a) iff $a^\mathcal {I}\in {C}^\mathcal {I}$. The assertion r(a, b) is satisfied by $\mathcal {I}$ iff $(a^\mathcal {I}, b^\mathcal {I}) \in {r}^\mathcal {I}$. Finally, $\mathcal {I}$ satisfies an RIA r⊑s iff $r^{\mathcal {I}}\subseteq s^{\mathcal {I}}$ and axioms Tra(r), Fun(r) iff the interpretation $r^{\mathcal {I}}$ is a transitive and a functional role, respectively. We say that $\mathcal {I}$ is a model of the KB $\mathcal {K}$, denoted by $\mathcal {I} \models \mathcal {K}$, iff $\mathcal {I}$ satisfies every axiom in $\mathcal {K}$. Finally, let $\mathcal {K}$ be a DL KB and α be an axiom, then $\mathcal {K}\models \alpha$ iff $\mathcal {I}\models \alpha$ for every model $\mathcal {I}$ of $\mathcal {K}$.
2.2 Symbolic Reasoning over Knowledge Bases
Reasoning with expressive DL KBs is a computationally hard task. Specifically, the instance checking problem, which, given $\mathcal {K}$, a concept C, and an individual x, determines whether x is an instance of C in $\mathcal {K}$ (denoted as $\mathcal {K} \models C(x)$) is non-deterministic (resp., double) exponential time complete for $\mathcal {SHOIQ}$ [20]. Given such high complexity and the additional challenges posed by incomplete and inconsistent data in real-world scenarios, practical applications often require the use of approximation algorithms.
To the best of our knowledge, HermiT [15] is the only reasoner that fully supports the OWL 2 standard. HermiT is based on a “hypertableau” calculus that addresses performance problems due to nondeterminism and model size—the primary sources of complexity in state-of-the-art OWL reasoners. HermiT was shown to outperform the previous reasoners, including Pellet [30], and Fact++ [33]. OWL2Bench [29] compares different reasoners across datasets and OWL profiles. Pellet and its extension Openllet were found to perform best in terms of runtime. JFact, the Java implementation of Fact++, performed worst on all the reasoning tasks across all OWL 2 profiles. While OWL2Bench assessed the reasoner's performance to detect inconsistent ontologies, they did not assess the robustness of reasoners, i.e., how well they answer queries on incomplete or inconsistent data.
2.3 Knowledge Graph Embeddings
Let $\mathcal {E}$ be the set of all entities and $\mathcal {R}$ the set of all relations. A knowledge graph (KG) $\mathcal {K} \subseteq \mathcal {E} \times \mathcal {R} \times \mathcal {E}$ is a set of triples (also called assertions) of the form (x, r, y) where $x, y\in \mathcal {E}$ are called head and tail entities, respectively, and $r \in \mathcal {R}$ depict the relationship between them. A Knowledge Graph Embedding (KGE) model is defined as a parameterized scoring function over KGs, depicted as $\phi _\Theta : \mathcal {K}\rightarrow \mathbb {R}$. where Θ denotes parameters, which often comprise entity embeddings $\mathbf {E} \in \mathbb {R}^{|\mathcal {E}| \times d_e}$, relation embeddings $\mathbf {R} \in \mathbb {R}^{|\mathcal {R}| \times d_r}$, and additional parameters (e.g., affine transformations, batch normalizations, convolutions). Since de = dr holds for many state-of-the-art models, we will use d to denote the number of embedding dimensions for both entities and relation types in a knowledge graph.
A plethora of KGE models have been developed over the last decade to address reasoning tasks over large symbolic knowledge graphs [9, 34]. These models aim to map entities and relations from the KG into continuous vector spaces, enabling efficient and scalable computation via algebraic operations. Most KGE approaches are primarily designed for the link prediction task, where the goal is to estimate the plausibility of a triple $(x, r, y) \in \mathcal {E} \times \mathcal {R} \times \mathcal {E}$. This is typically done via a scoring function $\phi _\Theta (x, r, y)$ parameterized by Θ, which produces a real-valued score $\hat{y}$ that reflects the likelihood (not necessarily calibrated) of the triple being valid [12].
Scoring functions vary across models: translational models like TransE [4] interpret relations as translations in vector space (i.e., $\vec{x} + \vec{r} \approx \vec{y}$), while bilinear models like DistMult [36] and ComplEx [32] employ multiplicative interactions, capturing symmetric and asymmetric patterns. Recent work has introduced more expressive representations based on Clifford algebras. Notably, Keci [12] generalizes models like DistMult and ComplEx by embedding entities and relations in Clifford spaces of the form Clp, q. DeCaL [31] extends this framework using degenerate Clifford algebras Clp, q, r, achieving state-of-the-art results on standard benchmarks.
Since most knowledge graphs encode only positive (i.e., true) facts, training KGE models necessitates the creation of negative samples typically via corrupting the head or tail entity in a triple. This is done using negative sampling techniques such as Bernoulli sampling [25], 1-vs-All, or K-vs-All strategies [27], which help the model differentiate between plausible and implausible triples. Learning is commonly performed using margin-based ranking losses or cross-entropy objectives, with regularization techniques to mitigate overfitting in large-scale settings.
KGEs have demonstrated remarkable versatility and effectiveness across a wide range of applications beyond link prediction. In drug discovery, embeddings assist in identifying novel drug-target interactions by modeling complex biomedical graphs [3]. In question answering, KGEs serve as soft reasoning engines that embed semantic relationships into the retrieval and inference pipeline [16]. In recommender systems, they enhance traditional collaborative filtering by leveraging multi-relational user-item graphs [8]. Moreover, recent trends explore explainable embeddings, temporal dynamics, and inductive generalization, pushing KGE techniques closer to deployment in real-world intelligent systems.
3 Approach
Ebr by itself is not an embedding model, but a reasoning framework that uses the representations learned by an embedding model to perform reasoning tasks like instance retrieval or concept learning. While KGE models focus on learning vector representations for entities and relations, EBR builds on top of these representations to approximate logical inference.
3.1 Knowledge Graph Embedding and Construction
Mapping description logic syntax to our neural semantics (see in Section 3.3) solely requires an engine that can accurately predict whether an assertion (x, r, y) is true. We map this task to computing whether the score assigned to an assertion is greater than or equal to a preset threshold γ. A key to achieving high accuracy on this task lies in the construction of a knowledge graph that renders the key assertions for our input knowledge base in such a way that accurate predictions can be carried out. To construct this knowledge graph $\mathcal {K}\subseteq \mathcal {E} \times \mathcal {R}\times \mathcal {E}$, we extract taxonomic axioms of the form $C(a)\equiv (x, \texttt{rdf:type}, C),\ r(x,y)\equiv (x,r,y)$, $C\sqsubseteq D\equiv (C, \texttt{rdfs:subClassOf}, D)$ and $r \sqsubseteq s\equiv (r, \texttt{rdfs:subPropertyOf}, s)$. The graph $\mathcal {G}$ is then used as input to a KGE model to learn embeddings for entities and relation types. This yields a trained KGE model $\phi _\Theta : \mathcal {E} \times \mathcal {R}\times \mathcal {E} \rightarrow \mathbb {V}^d$— where $\mathbb {V}^d$ is a vector space.
(1)
3.2 Prediction Mechanism
Once the model $\phi _\Theta$ is trained, we construct a neural link predictor $\phi : \mathcal {E} \times \mathcal {R} \times \mathcal {E} \rightarrow [0,1]$ which can assign a truth probability to any triple (x, r, y) from its domain. Given that the scores computed by $\phi _\Theta$ are not bound, we chose to use the sigmoid trick used in neural networks to translate scores into a range that can be interpreted as a probability. Consequently, we set $\phi (x, r, y) = \sigma (\phi _\Theta (x, r, y))$, where σ stands for the sigmoid function. A triple is then considered true in our neural interpretation if ϕ(x, r, y) is larger than a preset threshold γ. This is a key difference to symbolic reasoning (see Table 2 for details on the neural semantics). In particular, triples (x, r, y) found in $\mathcal {K}$ might be predicted to be false and hence not included in the neural interpretation of the input knowledge graph.
3.3 Mapping DL Syntax to Neural Semantics
The syntax and semantics for concepts in $\mathcal {SHOIQ}$ are provided in Table 1. We define a mapping from concept constructors in $\mathcal {SHOIQ}$ to their neural semantics in Table 2. For a given KB $ \mathcal {K}$, the domain $\Delta ^\mathcal {N} \subseteq \mathcal {E} \cup \mathcal {R}$ of the interpretation $\mathcal {N}$ computed by Ebr is the set of all class names, individual names and role names found in the axioms in $\mathcal {K}$.
| Construct | Syntax | Neural Semantics $\cdot ^{\mathcal {N}}$ |
|---|---|---|
| Atomic concept | A | $\lbrace x \mid \phi (x,\texttt{rdf:type},A) \ge \gamma \rbrace$ |
| Atomic role | r | {(x, y)∣ϕ(x, r, y) ≥ γ} |
| Top concept | ⊤ | $\Delta ^\mathcal {N}$ |
| Bottom concept | ⊥ | ∅ |
| Negation | ¬C | $\Delta ^\mathcal {N}\setminus C^{\mathcal {N}}$ |
| Conjunction | C⊓D | $C^{\mathcal {N}} \cap D^{\mathcal {N}}$ |
| Disjunction | C⊔D | $C^{\mathcal {N}} \cup D^{\mathcal {N}}$ |
| Existential restriction | ∃ r.C | $\lbrace x \mid \exists \ y \text{ s.t. } (x,y) \in r^{\mathcal {N}} \wedge y \in C^{\mathcal {N}}\rbrace$ |
| Universal restriction | ∀ r.C | $(\lnot (\exists r. \lnot C))^{\mathcal {N}}$ |
| Universal Role | U | $\Delta ^\mathcal {N}\times \Delta ^\mathcal {N}$ |
| Inverse Role | r− 1 | $\lbrace (y,x) \mid (x,y)\in r^{\mathcal {N}} \rbrace$ |
| Nominals | {o} | $\lbrace o^{\mathcal {N}}\rbrace$ |
| At least restriction | ≥ ns.C | $\lbrace a \mid \; | \lbrace b\in C^{\mathcal {N}} | (a,b) \in s^{\mathcal {N}} \rbrace | \ge n \rbrace$ |
| At most restriction | ≤ ns.C | $\lbrace a \mid \; | \lbrace b\in C^{\mathcal {N}}| (a,b) \in s^{\mathcal {N}} \rbrace | \le n \rbrace$ |
These mappings allow us to handle not only atomic concepts and roles but also more expressive axioms involving complex concept expressions. For example, consider the TBox axiom A⊓∃r.B⊑C⊔∀r.D, which asserts that individuals belonging to both A and those related via r to instances of B must also belong to either C or to those whose r-successors are all in D. In the neural setting, this axiom is interpreted as a set inclusion constraint: $(A^{\mathcal {N}} \cap \lbrace x \mid \exists y.\ (x, y) \in r^{\mathcal {N}} \wedge y \in B^{\mathcal {N}} \rbrace) \subseteq (C^{\mathcal {N}} \cup \lbrace x \mid \forall y.\ (x, y) \in r^{\mathcal {N}} \Rightarrow y \in D^{\mathcal {N}} \rbrace)$.
While such axioms are not explicitly encoded as triples in the knowledge graph, their components, such as class memberships and role assertions, are grounded via basic triples like :a rdf:type :A, :a :r :b, and :b rdf:type :B. The embedding-based interpretation $\mathcal {N}$ reconstructs the semantics of the full axiom by composing the neural representations of these grounded components, thus enabling reasoning over complex concept expressions in a continuous space.
4 Experimental Setup
Ebr is designed to improve the robustness of concept learning. In our experiments, we evaluate its performance on instance retrieval under varying levels of incompleteness and inconsistency, and further demonstrate that its reasoning capabilities generalize to concept learning as well.
Candidate concepts are generated using the refinement operator ρ from [11] by randomly sampling concepts from its refinement tree. The next section presents the datasets and evaluation metrics, followed by the experimental results and analysis.
4.1 Datasets
We evaluated our proposed approach on six benchmark datasets, including four large datasets (Carcinogenesis, Mutagenesis, Semantic Bible, and Vicodi) and two smaller datasets (Family and Father). These datasets cover a range of domains, from biological interactions to historical and familial relationships. Detailed statistics for each dataset are provided in Table 3.
| Dataset | |Ind.| | |Classes| | |Prop.| | |TBox| | |ABox| |
|---|---|---|---|---|---|
| Carcinogenesis | 22,372 | 142 | 4 | 144 | 74,223 |
| Mutagenesis | 14,145 | 86 | 5 | 82 | 47,722 |
| Semantic Bible | 724 | 48 | 29 | 56 | 3,106 |
| Vicodi | 33,238 | 194 | 10 | 204 | 116,181 |
| Family | 202 | 18 | 4 | 26 | 472 |
| Father | 6 | 4 | 1 | 3 | 4 |
4.2 Tasks
We evaluate Ebr across three main tasks to assess its robustness and effectiveness under different knowledge base conditions.
Task 1: Instance Retrieval. In the first task, we evaluate Ebr on standard instance retrieval using complete and consistent knowledge bases. The goal is to measure how accurately our reasoner retrieves instances of given class expressions compared to symbolic reasoners. We quantify performance using the Jaccard similarity, which compares the set of instances $\hat{y}$ retrieved by our reasoner with the ground-truth set y obtained from symbolic reasoners.3 The Jaccard similarity $J(\hat{y}, y)$ is defined as:
(2)
Task 2: Robustness to Noise and Incompleteness. The second task examines the performance of Ebr under noisy and incomplete knowledge bases. Starting from a consistent and correct knowledge base $\mathcal {K}$, we simulate noise by injecting $\nu |\mathcal {K}|$ random false axioms, where ν denotes the predefined noise ratio. To simulate incompleteness, we randomly remove $\nu |\mathcal {K}|$ axioms from $\mathcal {K}$. For concept learning, we focus on the inconsistent scenario and compare Ebr, against baseline reasoners.
Evaluation Protocol. We first choose a KGE model and integrate it into EBR to perform instance retrieval and concept learning across the scenarios described above. For all instance retrieval experiments, we use the Fast Instance Checker (FIC) reasoner from the DL-Learner framework [6, 10], which can support reasoning under inconsistency, making it a suitable reference for evaluating embedding-based retrieval. Other symbolic reasoners used include Pellet, HermiT, Openllet, JFact, and the Structural reasoner, the latter being a lightweight variant of FIC. For concept learning, we evaluate four state-of-the-art learners: OCEL and CELOE [6, 23] from the DL-Learner framework, CLIP [22], and EvoLearner (EVO) [17] with baseline reasoners in the backend and compare their performances (using the traditional F1-score [11]). All concept learners rely on FIC as their default reasoning component, ensuring consistency and comparability across models. Their performances are assessed using the traditional F1-score [11].
4.3 Hardware
All our experiments were carried out on a virtual machine with 2 NVIDIA H100-80C GPUs, each with 80 GB of memory. Note that the embedding computation only consumed approximately 16 GB of GPU memory on the biggest datasets (e.g., Vicodi).
5 Results and Discussion
In our experiments, Pellet, HermiT, Openllet, and JFact consistently exhibit identical performance for instance retrieval. Therefore, in this section, we report only the results of Pellet as representative of all four reasoners.
5.1 KGE Model Selection
We selected the KGE model and embedding dimensionality used throughout our experiments following a systematic protocol aimed at maximizing retrieval accuracy while maintaining a reasonable balance between model complexity and training cost. Each candidate KGE model was trained with embedding dimensions of 16, 32, 64, 128, and 256, and its instance retrieval performance within Ebr was assessed using the Jaccard similarity between the instances predicted by the Embedding-Based Reasoner (EBR) and those retrieved by the symbolic instance checker (FIC). The average Jaccard scores over all target expressions are summarized in Figure 1.
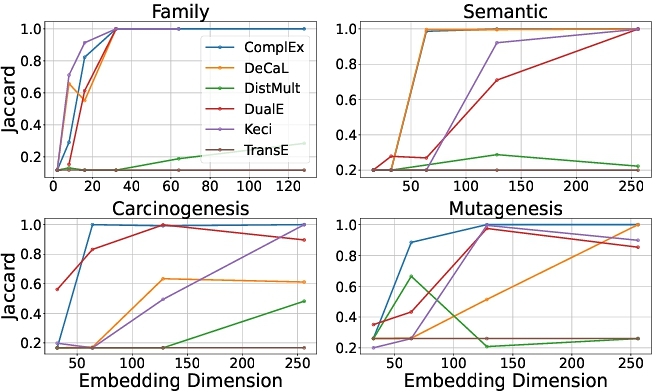
From the figure, it is evident that TransE and DistMult perform poorly–TransE never exceeds a Jaccard score of 0.2, while DistMult remains below 0.4–regardless of the embedding dimensionality. This suggests that the embeddings learned by these models are not sufficiently expressive to capture the relational and hierarchical semantics required for accurate instance retrieval within expressive ontologies. In contrast, other embedding models such as DeCaL, Keci, DualE [7], and ComplEx exhibit strong performance, with their Jaccard similarity steadily converging toward 1.0 as the embedding dimension increases. This indicates that Ebr can operate effectively with a wide range of expressive KGE models.
Based on these observations, we selected ComplEx with an embedding dimension of 128 as the default configuration for Ebr. This choice was motivated by three consistent findings from Figure 1: (i) ComplEx achieves the highest and most stable Jaccard scores across all datasets, (ii) performance improvements plateau beyond 128 dimensions, and (iii) the model remains computationally efficient at this size. As confirmed in Table 4, this configuration enables EBR to achieve perfect retrieval accuracy across all datasets and OWL concept types from dimension 128 onward.
5.2 Retrieval on Complete and Consistent Datasets
Table 4 reports the instance retrieval performance of Ebr across four error-free benchmark datasets. Performance improves steadily with larger embedding dimensions, reaching perfect Jaccard scores (1.00) for all concept types at d = 128 and beyond. The largest gains occur between d = 32 and d = 64, indicating that a minimum embedding capacity is needed to capture the ontological structure of these datasets.
For instance, in the Carcinogenesis dataset, accuracy for conjunctions (C⊓D) rises from 0.37 at d = 32 to 0.99 at d = 64, achieving perfection at d = 128. Similar trends hold for other complex concepts such as C⊔D, ∃r.C, and ∀r.C. Increasing d beyond 128 yields no meaningful improvement, confirming that d = 128 strikes an effective balance between accuracy and computational efficiency. The consistent results across all datasets further support the generality of this configuration.
An important advantage of Ebr is its robustness to the choice of the parameter γ, which governs the selection of individuals (see Table 2). Across all datasets, we observed that varying γ had a negligible impact on the Jaccard similarity, hence, on the set of retrieved instances. This makes Ebr easier to tune in practice, as it consistently retrieves correct instances without requiring fine-grained threshold calibration.
| Syntax | Carcinogenesis | Mutagenesis | ||||||
|---|---|---|---|---|---|---|---|---|
| d=32 | d=64 | d=128 | d=256 | d=32 | d=64 | d=128 | d=256 | |
| A | 0.00 | 1.00 | 1.00 | 1.00 | 0.20 | 0.82 | 0.99 | 1.00 |
| ¬A | 0.00 | 0.99 | 1.00 | 1.00 | 0.00 | 0.80 | 0.99 | 1.00 |
| C⊓D | 0.37 | 0.99 | 1.00 | 1.00 | 0.55 | 0.90 | 0.99 | 1.00 |
| C⊔D | 0.00 | 0.99 | 1.00 | 1.00 | 0.06 | 0.90 | 0.99 | 1.00 |
| ∃r.C | 0.00 | 0.99 | 1.00 | 1.00 | 0.00 | 0.78 | 0.99 | 1.00 |
| ∀r.C | 0.21 | 0.98 | 1.00 | 1.00 | 0.00 | 0.75 | 0.99 | 1.00 |
| ≥ ns.C | 0.00 | 0.97 | 1.00 | 1.00 | 0.02 | 0.90 | 0.99 | 1.00 |
| ≤ ns.C | 0.00 | 0.98 | 1.00 | 1.00 | 0.00 | 0.90 | 0.99 | 1.00 |
| {o} | 0.00 | 0.97 | 1.00 | 1.00 | 0.00 | 0.78 | 0.99 | 1.00 |
| Syntax | Semantic Bible | Family | ||||||
| d=16 | d=32 | d=64 | d=128 | d=2 | d=8 | d=16 | d=32 | |
| A | 0.00 | 0.00 | 0.98 | 1.00 | 0.00 | 0.00 | 0.92 | 1.00 |
| ¬A | 0.00 | 0.00 | 0.98 | 1.00 | 0.00 | 0.00 | 0.98 | 1.00 |
| C⊓D | 0.50 | 0.50 | 0.99 | 1.00 | 0.28 | 0.28 | 0.92 | 1.00 |
| C⊔D | 0.00 | 0.00 | 0.99 | 1.00 | 0.00 | 0.00 | 0.97 | 1.00 |
| ∃r.C | 0.25 | 0.28 | 0.94 | 1.00 | 0.00 | 0.00 | 0.51 | 1.00 |
| ∀r.C | 0.10 | 0.10 | 0.97 | 1.00 | 0.00 | 0.00 | 0.72 | 1.00 |
| ≥ ns.C | 0.00 | 0.13 | 0.99 | 1.00 | 0.38 | 0.38 | 0.43 | 1.00 |
| ≤ ns.C | 0.00 | 0.13 | 0.97 | 1.00 | 0.00 | 0.00 | 0.95 | 1.00 |
| {o} | 0.20 | 0.20 | 0.98 | 1.00 | 0.00 | 0.00 | 0.52 | 1.00 |
5.3 Retrieval on Incomplete Knowledge Bases
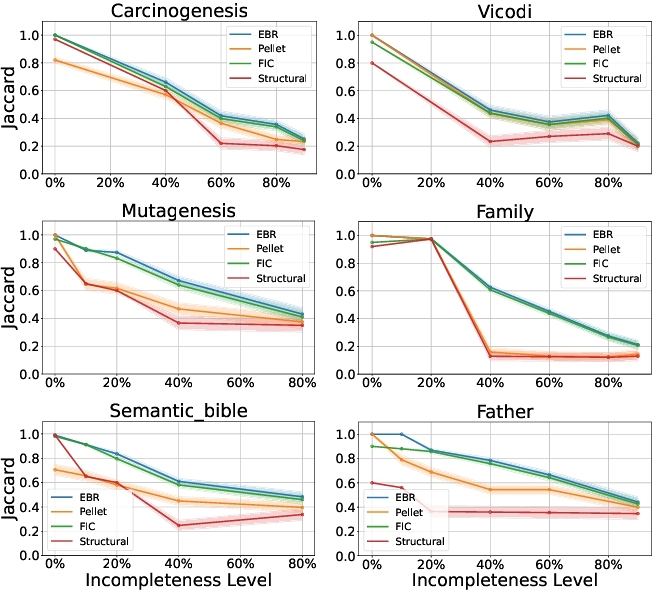
Here, we present the results of $\rm E{\small BR}$ along with state-of-the-art reasoners on all datasets. In Figure 3, we present the average Jaccard similarity scores with margins of error for each dataset across varying levels of incompleteness. In general, Ebr exhibits higher or comparable Jaccard similarity scores relative to other reasoners in most cases, particularly at higher levels of incompleteness. However, as the level of incompleteness increases, the performance of all reasoners declines. This is expected, as higher incompleteness typically leads to poorer retrieval performance. In this phase, removed instances are not tracked; therefore, the threshold is determined through the experiments. Therefore, given queries may not be related to removed instances, which explains why we can have an increase or the same performance for an increased level of incompleteness.
Table 5 reports the average runtime of each reasoner across datasets for the concept retrieval task. Overall, Ebr exhibits strong runtime efficiency, achieving the affordable execution times on smaller datasets such as Family and Father, and competitive performance on larger ones like Carcinogenesis and Vicodi. While symbolic reasoners such as HermiT and JFact show significantly higher runtimes, particularly on complex ontologies Ebr maintains a consistent balance between speed and scalability.
| Reasoner | Carci. | Muta. | Vicodi | Semantic | Family | Father |
|---|---|---|---|---|---|---|
| EBR | 10.3 | 8.5 | 78.1 | 8.4 | 0.1 | 0.01 |
| HermiT | 49.5 | 16.0 | 300.2 | 100. | 1.0 | 0.1 |
| Pellet | 10.1 | 2.5 | 80.2 | 6.2 | 1.5 | 0.01 |
| JFact | 12.3 | 2.2 | 100. | 20.9 | 4.5 | 0.04 |
| Openllet | 8.1 | 0.4 | 70.4 | 5.5 | 1.3 | 0.02 |
| FIC | 5.0 | 0.1 | 50.5 | 5.5 | 0.05 | 0.01 |
| Structural | 2.4 | 0.1 | 25.5 | 3.6 | 0.07 | 0.01 |
5.4 Retrieval on Noisy Knowledge Bases
| Carcinogenesis (10% Inconsistency) | ||||
|---|---|---|---|---|
| Pellet | EBR | Structural | FIC | |
| OCEL | * | 1.00 | 0.66 | 0.93 |
| CELOE | * | 1.00 | 0.87 | 0.93 |
| EVO | * | 1.00 | 0.77 ± 0.03 | 0.99 |
| CLIP | * | 1.00 | 0.87 | 0.93 |
| Vicodi (10% Inconsistency) | ||||
| Pellet | EBR | Structural | FIC | |
| OCEL | * | 0.36 ± 0.002 | 0.29 | 0.49 |
| CELOE | * | 0.55 ± 0.02 | 0.29 | 0.49 |
| EVO | * | 0.36 ± 0.002 | 0.29 | 0.49 ± 0.15 |
| CLIP | * | 0.55 ± 0.02 | 0.29 | 0.49 |
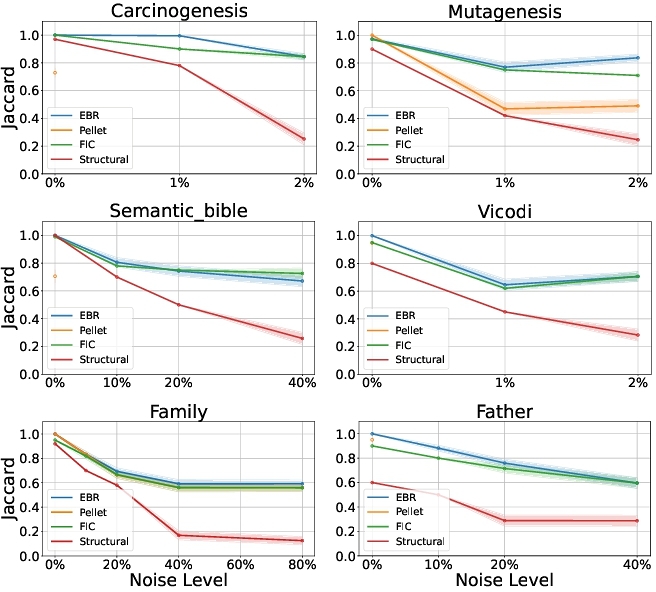
The general performance of all reasoners on noisy knowledge bases is illustrated in Figure 2. In the Carcinogenesis, Mutagenesis, and Vicodi datasets, we injected $1\%$ and $2\%$ noise, corresponding to at least 1,000 corrupted axioms per dataset. For smaller datasets, the noise ratios ranged between $10\%$ and $80\%$.
As shown in Figure 2, symbolic reasoners do not operate on most noisy datasets. Symbolic reasoners often fail on noisy datasets due to contradictions introduced by injected noise, which make knowledge bases inconsistent. In contrast, Ebr, along with FIC and the Structural reasoner, can handle such inconsistencies. Ebr shows strong robustness, achieving consistently high Jaccard scores and outperforming other reasoners on most datasets, except for a slight drop against FIC on the Semantic_Bible dataset. It also performs best on datasets without contradictions, like Mutagenesis and Family.
We further assessed the effectiveness of Ebr when integrated into concept learning frameworks on inconsistent knowledge bases. The results in Table 6 report the average F1-scores (and standard deviations where applicable) for several concept learners combined with different reasoning backends. Ebr maintained stable and high predictive performance across all learners. On the Carcinogenesis dataset, EBR achieved perfect F1-scores (1.00) across all learners, surpassing both FIC and Structural. On the more complex Vicodi dataset, EBR remained competitive with FIC, consistently outperforming the Structural reasoner. These results highlight that Ebr not only supports reasoning under inconsistencies but also enables reliable concept learning in scenarios where classical symbolic reasoners cannot operate.
6 Conclusion
We introduced Ebr, an embedding-based reasoner that leverages link prediction on knowledge graph embeddings to perform robust reasoning on inconsistent and incomplete Knowledge bases under the expressive $\mathcal {SHOIQ}$ Description Logic. Our experiments demonstrate that Ebr significantly outperforms traditional symbolic reasoners, which do not operate with inconsistencies. Our experiments show that with missing assertions in a given knowledge base, Ebr, using link prediction, can still recover the full set of individuals, which is not possible for any of the traditional reasoners.
Acknowledgments
This work has received funding from the European Union's Horizon Europe research and innovation programme under grant agreements No.101070305 and No.101073307 (Marie MarieSkłodowska-Curie). It has also been supported by the project WHALE (LFN 1-04), funded under the Lamarr Fellow Network programme by the Ministry of Culture and Science of North Rhine-Westphalia (MKW NRW). In addition, this work was supported by the German Federal Ministry of Research, Technology and Space (BMFTR) within the project KI-OWL under grant No. 01IS24057B.
References
- Franz Baader. 2003. The description logic handbook: Theory, implementation and applications. Cambridge university press.
- Yushi Bai, Xin Lv, Juanzi Li, and Lei Hou. 2023. Answering complex logical queries on knowledge graphs via query computation tree optimization. In International Conference on Machine Learning. PMLR, 1472–1491.
- Stephen Bonner, Ian P Barrett, Cheng Ye, Rowan Swiers, Ola Engkvist, Charles Tapley Hoyt, and William L Hamilton. 2022. Understanding the performance of knowledge graph embeddings in drug discovery. Artificial Intelligence in the Life Sciences 2 (2022), 100036.
- Antoine Bordes, Nicolas Usunier, Alberto Garcia-Duran, Jason Weston, and Oksana Yakhnenko. 2013. Translating embeddings for modeling multi-relational data. Advances in neural information processing systems 26 (2013).
- Ronald Brachman and Hector Levesque. 2004. Knowledge representation and reasoning. Elsevier.
- Lorenz Bühmann, Jens Lehmann, and Patrick Westphal. 2016. DL-Learner-A framework for inductive learning on the Semantic Web. Journal of Web Semantics 39 (2016), 15–24.
- Zongsheng Cao, Qianqian Xu, Zhiyong Yang, Xiaochun Cao, and Qingming Huang. 2021. Dual quaternion knowledge graph embeddings. In Proceedings of the AAAI conference on artificial intelligence, Vol. 35. 6894–6902.
- Nurendra Choudhary, Nikhil Rao, Sumeet Katariya, Karthik Subbian, and Chandan K Reddy. 2021. Self-supervised hyperboloid representations from logical queries over knowledge graphs. In Proceedings of the Web Conference 2021. 1373–1384.
- Yuanfei Dai, Shiping Wang, Neal N Xiong, and Wenzhong Guo. 2020. A survey on knowledge graph embedding: Approaches, applications and benchmarks. Electronics 9, 5 (2020), 750.
- Caglar Demir, Alkid Baci, N'Dah Jean Kouagou, Leonie Nora Sieger, Stefan Heindorf, Simon Bin, Lukas Bl"ubaum, Alexander Bigerl, and Axel-Cyrille Ngonga Ngomo. 2025. Ontolearn—A Framework for Large-scale OWL Class Expression Learning in Python. Journal of Machine Learning Research 26, 63 (2025), 1–6. http://jmlr.org/papers/v26/24-1113.html
- Caglar Demir and Axel-Cyrille Ngonga Ngomo. 2023. Neuro-Symbolic Class Expression Learning.. In IJCAI. 3624–3632.
- Caglar Demir and Axel-Cyrille Ngonga Ngomo. 2023. Clifford Embeddings–A Generalized Approach for Embedding in Normed Algebras. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 567–582.
- Caglar Demir, Michel Wiebesiek, Renzhong Lu, Axel-Cyrille Ngonga Ngomo, and Stefan Heindorf. 2023. LitCQD: Multi-hop Reasoning in Incomplete Knowledge Graphs with Numeric Literals. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Springer, 617–633.
- Tim Dettmers, Pasquale Minervini, Pontus Stenetorp, and Sebastian Riedel. 2018. Convolutional 2D Knowledge Graph Embeddings. In AAAI. AAAI Press, 1811–1818.
- Birte Glimm, Ian Horrocks, Boris Motik, Giorgos Stoilos, and Zhe Wang. 2014. HermiT: an OWL 2 reasoner. Journal of automated reasoning 53 (2014), 245–269.
- Will Hamilton, Payal Bajaj, Marinka Zitnik, Dan Jurafsky, and Jure Leskovec. 2018. Embedding logical queries on knowledge graphs. Advances in neural information processing systems 31 (2018).
- Stefan Heindorf, Lukas Blübaum, Nick Düsterhus, Till Werner, Varun Nandkumar Golani, Caglar Demir, and Axel-Cyrille Ngonga Ngomo. 2022. Evolearner: Learning description logics with evolutionary algorithms. In Proceedings of the ACM Web Conference 2022. 818–828.
- Pascal Hitzler, Markus Krotzsch, and Sebastian Rudolph. 2009. Foundations of semantic web technologies. Chapman and Hall/CRC.
- Ian Horrocks, Peter F Patel-Schneider, and Frank Van Harmelen. 2003. From SHIQ and RDF to OWL: The making of a web ontology language. Journal of web semantics 1, 1 (2003), 7–26.
- Yevgeny Kazakov. 2008. RIQ and SROIQ Are Harder than SHOIQ. In Principles of Knowledge Representation and Reasoning: Proceedings of the Eleventh International Conference, KR 2008, Sydney, Australia, September 16-19, 2008, Gerhard Brewka and Jérôme Lang (Eds.). AAAI Press, 274–284. http://www.aaai.org/Library/KR/2008/kr08-027.php
- C Maria Keet. 2018. An introduction to ontology engineering. (2018).
- N'Dah Jean Kouagou, Stefan Heindorf, Caglar Demir, and Axel-Cyrille Ngonga Ngomo. 2022. Learning concept lengths accelerates concept learning in ALC. In European Semantic Web Conference. Springer, 236–252.
- Jens Lehmann and Pascal Hitzler. 2010. Concept learning in description logics using refinement operators. Machine Learning 78 (2010), 203–250.
- Maximilian Nickel, Kevin Murphy, Volker Tresp, and Evgeniy Gabrilovich. 2015. A review of relational machine learning for knowledge graphs. Proc. IEEE 104, 1 (2015), 11–33.
- Jing Qian, Gangmin Li, Katie Atkinson, and Yong Yue. 2021. Understanding negative sampling in knowledge graph embedding. (2021).
- Hongyu Ren and Jure Leskovec. 2020. Beta embeddings for multi-hop logical reasoning in knowledge graphs. Advances in Neural Information Processing Systems 33 (2020), 19716–19726.
- Daniel Ruffinelli, Samuel Broscheit, and Rainer Gemulla. 2020. You CAN Teach an Old Dog New Tricks! On Training Knowledge Graph Embeddings. In ICLR. OpenReview.net.
- Uli Sattler, Robert Stevens, and Phillip Lord. 2014. How does a reasoner work?Ontogenesis (2014).
- Gunjan Singh, Sumit Bhatia, and Raghava Mutharaju. 2020. OWL2Bench: A Benchmark for OWL 2 Reasoners. In ISWC (2)(Lecture Notes in Computer Science, Vol. 12507). Springer, 81–96.
- Evren Sirin, Bijan Parsia, Bernardo Cuenca Grau, Aditya Kalyanpur, and Yarden Katz. 2007. Pellet: A practical owl-dl reasoner. Journal of Web Semantics 5, 2 (2007), 51–53.
- Louis Mozart Kamdem Teyou, Caglar Demir, and Axel-Cyrille Ngonga Ngomo. 2024. Embedding Knowledge Graphs in Degenerate Clifford Algebras. arXiv preprint arXiv:2402.04870 (2024).
- Théo Trouillon, Christopher R Dance, Éric Gaussier, Johannes Welbl, Sebastian Riedel, and Guillaume Bouchard. 2017. Knowledge graph completion via complex tensor factorization. Journal of Machine Learning Research 18, 130 (2017), 1–38.
- Dmitry Tsarkov and Ian Horrocks. 2006. FaCT++ description logic reasoner: System description. In International joint conference on automated reasoning. Springer, 292–297.
- Meihong Wang, Linling Qiu, and Xiaoli Wang. 2021. A survey on knowledge graph embeddings for link prediction. Symmetry 13, 3 (2021), 485.
- David Werner, Nuno Silva, Christophe Cruz, and Aurelie Bertaux. 2014. Using DL-reasoner for hierarchical multilabel classification applied to economical e-news. In 2014 Science and Information Conference. IEEE, 313–320.
- Bishan Yang, Wen-tau Yih, Xiaodong He, Jianfeng Gao, and Li Deng. 2014. Embedding entities and relations for learning and inference in knowledge bases. arXiv preprint arXiv:1412.6575 (2014).
Footnote
1 https://dbpedia.org/ontology/
2 https://github.com/Louis-Mozart/Embedding-Based-Reasoner
3Note that all symbolic reasoners used in this setting yield identical results under consistent and complete data.

This work is licensed under a Creative Commons Attribution 4.0 International License.
K-CAP '25, Dayton, OH, USA
© 2025 Copyright held by the owner/author(s).
ACM ISBN 979-8-4007-1867-0/25/12.
DOI: https://doi.org/10.1145/3731443.3771348