Global-Local Item Embedding for Temporal Set Prediction
DOI: https://doi.org/10.1145/3460231.3478844
RecSys '21: Fifteenth ACM Conference on Recommender Systems, Amsterdam, Netherlands, September 2021
Temporal set prediction is becoming increasingly important as many companies employ recommender systems in their online businesses, e.g., personalized purchase prediction of shopping baskets. While most previous techniques have focused on leveraging a user's history, the study of combining it with others’ histories remains untapped potential. This paper proposes Global-Local Item Embedding (GLOIE) that learns to utilize the temporal properties of sets across whole users as well as within a user by coining the names as global and local information to distinguish the two temporal patterns. GLOIE uses Variational Autoencoder (VAE) and dynamic graph-based model to capture global and local information and then applies attention to integrate resulting item embeddings. Additionally, we propose to use Tweedie output for the decoder of VAE as it can easily model zero-inflated and long-tailed distribution, which is more suitable for several real-world data distributions than Gaussian or multinomial counterparts. When evaluated on three public benchmarks, our algorithm consistently outperforms previous state-of-the-art methods in most ranking metrics.
ACM Reference Format:
Seungjae Jung, Young-Jin Park, Jisu Jeong, Kyung-Min Kim, Hiun Kim, Minkyu Kim, and Hanock Kwak. 2021. Global-Local Item Embedding for Temporal Set Prediction. In Fifteenth ACM Conference on Recommender Systems (RecSys '21), September 27-October 1, 2021, Amsterdam, Netherlands. ACM, New York, NY, USA, 6 pages. https://doi.org/10.1145/3460231.3478844
1 INTRODUCTION
Many recommendation tasks can be viewed as a problem of predicting the next set given the sequence of sets, e.g., predicting the next basket in online markets and the next playlist in streaming services. Previous works mainly focused on the local information (a given user's history), applying RNNs [2, 4, 20] or self-attention [21] to learn the temporal tendency of a sequence of sets within a user. From the recommender system point of view, temporal set prediction can have a sparsity problem as many users interact with only a small number of items. Throughout the recommender system literature, the sparsity problem has been dealt with low-rank approximation or collaborative filtering [11, 15, 16, 17]. However, such attempts have been less explored in temporal set prediction literature.
In this paper, we propose Global-Local Item Embedding (GLOIE) that integrates global and local information for temporal set prediction. To capture the global information, we utilize the Variational Autoencoders (VAEs) [10, 12] which are effective on noisy and sparse data. GLOIE then integrates the local embeddings, that are learned through dynamic graphs [21], with global embeddings by using an attention method. In addition, we enhance the performance of GLOIE by using Tweedie distribution for the likelihood of VAE instead of Gaussian or multinomial distributions. We show that purchase logs follow zero-inflated and long-tail distributions similar to the Tweedie distribution.
We conduct experiments on three public benchmarks, i.e. Dunnhumby Carbo, TaoBao, and Tags-Math-Sx. Empirical results demonstrate that the proposed method outperforms state-of-the-art methods on most metrics. The main contributions of the paper are summarized as follows:

- We propose GLOIE which differentiate global and local information and integrates them.
- We claim that using Tweedie output for VAE decoder is beneficial as it naturally models two properties of data distributions from temporal set prediction problems: zero-inflated and long-tailed.
- We achieve state-of-the-art performance on three public benchmarks.
2 PRELIMINARIES
2.1 Problem Definition
Let $\mathcal {U} = \lbrace u_1, u_2, \dots, u_N \rbrace$ be set of users and $\mathcal {E} = \lbrace e_1, e_2, \dots, e_M \rbrace$ be set of items. Given a user ui’s sequence of sets , our goal is to predict next set $S_i^{T_i + 1}$. Each set $S_i^k$ can also be represented as a binary vector form $\mathbf {v}_i^k$, where each element
.
is a indicator function which returns 1 if x is true and 0 otherwise. We will use the set notation $S_i^k$ and $\mathbf {v}_i^k$ interchangeably to denote user ui’s k-th set.
2.2 Variational Autoencoders
Variational Autoencoders (VAEs) [10, 13] are a class of deep generative models. VAEs provide latent structures that can nicely explain the observed data (e.g., customer's purchase history). Formally speaking, VAEs find the latent variables (z) that maximize the evidence lower bound (ELBO), a surrogate objective function for the maximum likelihood estimation of the given observation x:
(1)
Encoders are commonly structured by multilayer perceptrons (MLPs) that produce Gaussian distributions over the latent variable z. On the other hand, decoders are designed to have different probability distributions of output layer depending on the characteristics of datasets. For example, Gaussian distribution and multinomial distribution are often used to represent the real-valued continuous and binary data, respectively.
3 METHOD
3.1 Learning Global-Local Information by VAE
We are interested in modeling other users’ history as well as the given user's history. We proceed with this under the VAE framework. However, a difficulty arises: every user has a different length of the sequence of sets. To resolve this, we sum time decayed sequence of sets.
(2)
(3)
As most people interact with a few items, vi contains many 0s and so does xi. However, the reconstructed vector $\hat{\mathbf {x}}_i$ generated from the following process:
(4)
Note that Hu et al. [5]’s Personalized Item Frequency (PIF) is similar to our sum of time decayed vectors. However, since their work is based on K-Nearest Neighbor, two shortcomings arise: 1) the inference time grows cubic with the number of users and 2) they cannot use features unlike traditional deep learning approaches.
3.2 Tweedie Output on Decoder
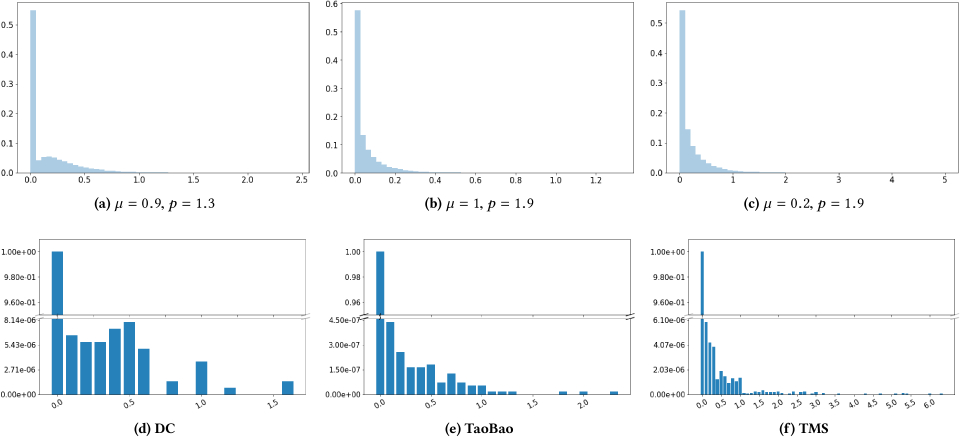
When training VAE, using gaussian output on p(x∣z) is a straightforward option. However, the distributions of the data generated from temporal set prediction problems are zero-inflated and long-tailed as shown in Figure 2.
Tweedie distribution is a special case of exponential dispersion model (EDM) with a power parameter p and the variance function V(μ) = μp [6]. Tweedie distribution with 1 < p < 2 corresponds to a class of compound Poisson distributions [7]. Consider two step sampling process N ∼ Poisson(λ) and Xi ∼ Gamma(α, β) for λ, α, β > 0 and i = 1, …, N. Now we define a random variable Z as follows:
(5)
It is straightforward that the distribution defined by Equation (5) is zero-inflated for small enough λ and long-tailed as Z is addition of Xi ∼ Gamma(α, β) for N > 0. Hence using Tweedie output on VAE's decoder for temporal set prediction is beneficial as Tweedie distribution easily captures the properties of distributions that are shown in Figure 2.
Learning the mean parameter μ and the power parameter p of Tweedie distribution via maximum likelihood is easy. Minimizing
(6)
A line of works chose distributions other than Gaussian or Bernoulli on matrix factorization and VAE [3, 12, 18]. Poisson distribution or multinomial distribution are usual choices. This paper is the first attempt to apply Tweedie distribution for VAE's decoder output to the best of our knowledge.
3.3 Integrating Global-Local Information
Though VAE with Tweedie output is already competent, it tends to underestimate a user's preference for the frequently interacted items. This tendency owes to the learning objective of VAE as the model has to maximize the likelihood of 0 for never interacted items. This sometimes sacrifices the ability to maximize the likelihood of values of interacted items. Hence, we integrate item embeddings of frequently interacted items which are learned by state-of-the-art models to our VAE. We use DNNTSP [21] as it is the state-of-the-art method. DNNTSP makes user-dependent embeddings of items that are interacted at least once via dynamic graph neural networks. We denote zij as the embedding of user ui for item ej.
When it comes to combining VAE with embeddings zij, a problem arises: the reconstructed value $\hat{\mathbf {x}}_{ij}$ of Equation (4) is a scalar while learned embedding zij is a vector. Hence, to match the size between $\hat{\mathbf {x}}_{ij}$ and zij, we simply multiply a vector w*, which is of same size as zij, to $\hat{\mathbf {x}}_{ij}$. We defer the discussion on the selection of w* to latter part of this section.
Now we combine updated embedding with $\hat{\mathbf {x}}_{ij} \cdot \mathbf {w}^*$s and zijs. The updated embedding $\tilde{\mathbf {z}}_{ij}$ is defined as
(7)
(8)
Lastly, we calculate the affinity of a user ui to item ej by
(9)
(10)
We now going back to the selection of w* in Equation (7). We set w* = w0 in Equation (9) though we can set w* as a learnable parameter. If we set w* = w0, Equation (9) becomes $ \hat{\mathbf {y}}_{ij} = \sigma \left(\hat{\mathbf {x}}_{ij} \cdot \mathbf {w}_0^T \mathbf {w}_0 + b_0 \right)$ for non-interacted item $e_j \notin \bigcup _k S_i^k$, hence it preserves the order of affinity that is learned by VAE. We also run experiments with learnable parameter w* but the performance was on par with w* = w0.
4 EXPERIMENTS
4.1 Benchmarks
| Dataset | # of users | # of sets | # of elements | #E/S | #S/U | #E/U |
|---|---|---|---|---|---|---|
| DC | 9,010 | 42,905 | 217 | 1.52 | 4.76 | 5.44 |
| TaoBao | 113,347 | 628,618 | 689 | 1.10 | 5.55 | 4.96 |
| TMS | 15,726 | 243,394 | 1,565 | 2.19 | 15.48 | 18.05 |
We evaluate our method on three public benchmarks: Dunnhumby Carbo (DC), TaoBao, and Tags-Math-Sx (TMS). We partitioned each dataset into train, validation and test into 70%, 10% and 20% respectively following Yu et al. [21]. See Table 1 for statistics of benchmarks.
4.2 Compared Methods
We compare four methods: Toppop, PersonalToppop, Sets2Sets and DNNTSP.
Toppop simply serves the items that are interacted the most across all users. PersonalToppop serves the items that the given user interacted with the most. Sets2Sets uses encoder-decoder framework to predict the next set [4]. Set embeddings are made by pooling operation and set-based attention is used to model temporal correlation relation. This method also models repeated elements. DNNTSP is composed of three components: Element Relationship Learning (ERL), Temporal Dependency Learning (TDL) and Gated Information Fusing. ERL is simply a dynamic weighted graph neural networks. TDL captures temporal dependency. By Gated Information Fusing each user shares the embeddings of uninteracted items. Hence DNNTSP can be seen as an ensemble of model which learns local information and Toppop model.
4.3 Results & Analyses
The results of our evaluation on three public benchmarks are shown in Table 2. We consider three metrics: Recall, Normalized Discounted Cumulative Gain (NDCG) and Personal Hit Ratio (PHR). PHR@K is calculated as where N′ is the number of test users, $\hat{S}_i$ is the predicted top-K elements, and Si is the ground truth set.
We trained VAE for 30 epochs and then trained DNNTSP for 30 epochs. We used only one layer for the VAEs across all benchmarks. For the decay factor in Equation (2), we set τ = 0.6. As illustrated in Figure 3, τ = 0.6 shows the best performance on TaoBao dataset. We empirically observe that τ = 0.6 could provide decent results across all metrics on the other datasets as well. The dimension of latent space is 128 for DC and TaoBao, and 512 for TMS. We used Adam optimizer [9] with learning rate 0.001.
Across all benchmarks and metrics, GLOIE with Tweedie output outperforms or is on par with all compared methods. Especially, GLOIE with Tweedie output outperforms the other methods on all metrics on DC and TaoBao datasets. We can see that GLOIE with Tweedie outperforms DNNTSP on every metric when K = 10 which means that the embeddings learned by VAE are richly used as well as the embeddings learned by DNNTSP.
One thing to remark is that VAE with Tweedie output shows comparable performance to all compared methods on most metrics. Given that the number of items a user interacted with is 5.44, 4.96, and 18.05 respectively in DC, TaoBao, and TMS, this shows that VAE with Tweedie output captures the preference of users to non-interacted items.
To investigate the effectiveness of the attention-based integration method illustrated in Equation (8), we compared GLOIE with attention to the one with itemwise learnable weight similar to the method proposed in Yu et al. [21]. For overall datasets and metrics, we could observe performance gains: 3.09%, 0.45%, 0.92% improvement of NDCG@10 on DC, Taobao, and TMS, respectively.
Lastly, we note that the selection of output distribution of decoder on VAE largely affects the performance. We empirically show that both Gaussian and multinomial outputs do not fit temporal set prediction problems even though Gaussian is a popular choice for VAE and multinomial is a common choice in recommender system literature after the advent of VAECF [12].
| Dataset | Model | k = 10 | k = 20 | k = 40 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Recall | NDCG | PHR | Recall | NDCG | PHR | Recall | NDCG | PHR | ||
| DC | Toppop | 0.1618 | 0.0880 | 0.2274 | 0.2475 | 0.1116 | 0.3289 | 0.3940 | 0.1448 | 0.4997 |
| PersonalToppop | 0.4104 | 0.3174 | 0.5031 | 0.4293 | 0.3270 | 0.5258 | 0.4747 | 0.3332 | 0.5785 | |
| Sets2Sets | 0.4488 | 0.3136 | 0.5458 | 0.5143 | 0.3319 | 0.6162 | 0.6017 | 0.3516 | 0.7005 | |
| DNNTSP | 0.4564 | 0.3165 | 0.5557 | 0.5294 | 0.3369 | 0.6272 | 0.6180 | 0.3568 | 0.7165 | |
| VAE - Gaussian | 0.1618 | 0.0882 | 0.2274 | 0.2507 | 0.1128 | 0.3333 | 0.3847 | 0.1430 | 0.4903 | |
| VAE - Multinomial | 0.1602 | 0.0850 | 0.2230 | 0.2492 | 0.1097 | 0.3311 | 0.3767 | 0.1387 | 0.4786 | |
| VAE - Tweedie | 0.4166 | 0.3000 | 0.5108 | 0.5122 | 0.3267 | 0.6062 | 0.6217 | 0.3517 | 0.7088 | |
| GLOIE - Gaussian | 0.3108 | 0.2349 | 0.3971 | 0.3738 | 0.2526 | 0.4664 | 0.4545 | 0.2706 | 0.5563 | |
| GLOIE - Multinomial | 0.3265 | 0.2465 | 0.4143 | 0.3870 | 0.2633 | 0.4798 | 0.4615 | 0.2803 | 0.5602 | |
| GLOIE - Tweedie | 0.4658 | 0.3264 | 0.5613 | 0.5415 | 0.3477 | 0.6351 | 0.6428 | 0.3708 | 0.7288 | |
| TaoBao | Toppop | 0.1567 | 0.0784 | 0.1613 | 0.2494 | 0.1019 | 0.2545 | 0.3679 | 0.1264 | 0.3745 |
| PersonalToppop | 0.2190 | 0.1535 | 0.2230 | 0.2260 | 0.1554 | 0.2306 | 0.2433 | 0.1590 | 0.2484 | |
| Sets2Sets | 0.2811 | 0.1495 | 0.2868 | 0.3649 | 0.1710 | 0.3713 | 0.4672 | 0.1922 | 0.4739 | |
| DNNTSP | 0.3035 | 0.1841 | 0.3095 | 0.3811 | 0.2039 | 0.3873 | 0.4776 | 0.2238 | 0.4843 | |
| VAE - Gaussian | 0.1592 | 0.0750 | 0.1635 | 0.2480 | 0.0974 | 0.2530 | 0.3665 | 0.1219 | 0.3727 | |
| VAE - Multinomial | 0.1588 | 0.0798 | 0.1634 | 0.2494 | 0.1027 | 0.2545 | 0.3660 | 0.1268 | 0.3723 | |
| VAE - Tweedie | 0.2954 | 0.1939 | 0.3006 | 0.3775 | 0.2148 | 0.3827 | 0.4768 | 0.2353 | 0.4822 | |
| GLOIE - Gaussian | 0.2982 | 0.1768 | 0.3044 | 0.3790 | 0.1973 | 0.3851 | 0.4769 | 0.2175 | 0.4835 | |
| GLOIE - Multinomial | 0.2980 | 0.1791 | 0.3040 | 0.3783 | 0.1995 | 0.3846 | 0.4750 | 0.2195 | 0.4819 | |
| GLOIE - Tweedie | 0.3099 | 0.2007 | 0.3152 | 0.3917 | 0.2216 | 0.3972 | 0.4868 | 0.2412 | 0.4924 | |
| TMS | Toppop | 0.2627 | 0.1627 | 0.4619 | 0.3902 | 0.2017 | 0.6243 | 0.5605 | 0.2448 | 0.8007 |
| PersonalToppop | 0.4508 | 0.3464 | 0.6440 | 0.5274 | 0.3721 | 0.7146 | 0.5495 | 0.3771 | 0.7374 | |
| Sets2Sets | 0.4748 | 0.3782 | 0.6933 | 0.5601 | 0.4061 | 0.7594 | 0.6627 | 0.4321 | 0.8570 | |
| DNNTSP | 0.4693 | 0.3473 | 0.6825 | 0.5826 | 0.3839 | 0.7880 | 0.6840 | 0.4097 | 0.8748 | |
| VAE - Gaussian | 0.2731 | 0.1919 | 0.4660 | 0.3913 | 0.2288 | 0.6195 | 0.5496 | 0.2688 | 0.7813 | |
| VAE - Multinomial | 0.2548 | 0.1615 | 0.4431 | 0.3830 | 0.2001 | 0.6020 | 0.5437 | 0.2412 | 0.7740 | |
| VAE - Tweedie | 0.4661 | 0.3744 | 0.6548 | 0.5579 | 0.4040 | 0.7432 | 0.6663 | 0.4316 | 0.8341 | |
| GLOIE - Gaussian | 0.1345 | 0.0833 | 0.2486 | 0.2363 | 0.1155 | 0.4018 | 0.4014 | 0.1570 | 0.6033 | |
| GLOIE - Multinomial | 0.1479 | 0.1029 | 0.2797 | 0.2192 | 0.1252 | 0.3872 | 0.3259 | 0.1524 | 0.5362 | |
| GLOIE - Tweedie | 0.4860 | 0.3823 | 0.6863 | 0.5868 | 0.4144 | 0.7753 | 0.6926 | 0.4418 | 0.8538 | |

5 CONCLUSION
This paper proposes Global-Local Item Embedding (GLOIE) that learns to utilize the temporal properties of sets across whole users as well as within a user. The proposed model learns global-local information by maximizing ELBO of the sum of time decayed vectors under the VAE framework and integrates local embeddings learned by dynamic graph neural networks. As users with similar histories are reconstructed to close vectors, we could model the preference of the given user for a non-interacted item if other users with similar histories frequently interacted with the item. Data analysis and empirical results show that using Tweedie output for VAE's decoder is effective for modeling temporal set prediction. The proposed method achieves state-of-the-art results by considering global information which is less explored in temporal set prediction literature.
Though the proposed VAE is powerful in itself, there is some room for improvement. Instead of using the sum of time decayed vector, we can model change of sets in continuous time by Neural ODE [1, 14]. Finding an appropriate form of prior that captures long-tailed distribution for the temporal set prediction can also be a future direction. Graph modality can also be used [8]. Last but not least, searching for better ways to integrating embeddings learned by VAE and embeddings learned by other algorithms which focus on local information is also an important future work.
REFERENCES
- Ricky T. Q. Chen, Yulia Rubanova, Jesse Bettencourt, and David K Duvenaud. 2018. Neural Ordinary Differential Equations. In Advances in Neural Information Processing Systems, S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett (Eds.), Vol. 31. Curran Associates, Inc.https://proceedings.neurips.cc/paper/2018/file/69386f6bb1dfed68692a24c8686939b9-Paper.pdf
- Edward Choi, Mohammad Taha Bahadori, Andy Schuetz, Walter F Stewart, and Jimeng Sun. 2016. Doctor ai: Predicting clinical events via recurrent neural networks. In Machine learning for healthcare conference. PMLR, 301–318.
- Prem Gopalan, Jake M. Hofman, and David M. Blei. 2015. Scalable Recommendation with Hierarchical Poisson Factorization. In Proceedings of the Thirty-First Conference on Uncertainty in Artificial Intelligence (Amsterdam, Netherlands) (UAI’15). AUAI Press, Arlington, Virginia, USA, 326–335.
- Haoji Hu and Xiangnan He. 2019. Sets2sets: Learning from sequential sets with neural networks. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1491–1499.
- Haoji Hu, Xiangnan He, Jinyang Gao, and Zhi-Li Zhang. 2020. Modeling personalized item frequency information for next-basket recommendation. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. 1071–1080.
- Bent Jørgensen. 1987. Exponential Dispersion Models. Journal of the Royal Statistical Society. Series B (Methodological) 49, 2(1987), 127–162. http://www.jstor.org/stable/2345415
- Bent Jørgensen. 1997. The Theory of Dispersion Models. Chapman and Hall/CRC.
- Kyung-Min Kim, Dong-Hyun Kwak, Hanock Kwak, Young-Jin Park, Sangkwon Sim, Jae-Han Cho, Minkyu Kim, Jihun Kwon, Nako Sung, and Jung-Woo Ha. 2019. Tripartite Heterogeneous Graph Propagation for Large-scale Social Recommendation. In Proceedings of ACM RecSys 2019 Late-Breaking Results, Marko Tkalcic and Sole Pera (Eds.). http://ceur-ws.org/Vol-2431/paper12.pdf
- Diederik P. Kingma and Jimmy Ba. 2015. Adam: A Method for Stochastic Optimization. In International Conference on Learning Representations, Yoshua Bengio and Yann LeCun (Eds.). http://arxiv.org/abs/1412.6980
- Diederik P. Kingma and Max Welling. 2014. Auto-Encoding Variational Bayes. In International Conference on Learning Representations, Yoshua Bengio and Yann LeCun (Eds.). https://openreview.net/forum?id=33X9fd2-9FyZd
- Yehuda Koren. 2008. Factorization Meets the Neighborhood: A Multifaceted Collaborative Filtering Model. In Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Las Vegas, Nevada, USA) (KDD ’08). Association for Computing Machinery, New York, NY, USA, 426–434. https://doi.org/10.1145/1401890.1401944
- Dawen Liang, Rahul G Krishnan, Matthew D Hoffman, and Tony Jebara. 2018. Variational autoencoders for collaborative filtering. In Proceedings of the 2018 world wide web conference. 689–698.
- Danilo Jimenez Rezende, Shakir Mohamed, and Daan Wierstra. 2014. Stochastic backpropagation and approximate inference in deep generative models. In International conference on machine learning. PMLR, 1278–1286.
- Yulia Rubanova, Ricky T. Q. Chen, and David K Duvenaud. 2019. Latent Ordinary Differential Equations for Irregularly-Sampled Time Series. In Advances in Neural Information Processing Systems, H. Wallach, H. Larochelle, A. Beygelzimer, F. d'Alché-Buc, E. Fox, and R. Garnett (Eds.), Vol. 32. Curran Associates, Inc.https://proceedings.neurips.cc/paper/2019/file/42a6845a557bef704ad8ac9cb4461d43-Paper.pdf
- Ruslan Salakhutdinov and Andriy Mnih. 2007. Probabilistic Matrix Factorization. In Proceedings of the 20th International Conference on Neural Information Processing Systems (Vancouver, British Columbia, Canada) (NIPS’07). Curran Associates Inc., Red Hook, NY, USA, 1257–1264.
- Badrul Sarwar, George Karypis, Joseph Konstan, and John Riedl. 2001. Item-Based Collaborative Filtering Recommendation Algorithms. In Proceedings of the 10th International Conference on World Wide Web (Hong Kong, Hong Kong) (WWW ’01). Association for Computing Machinery, New York, NY, USA, 285–295. https://doi.org/10.1145/371920.372071
- Nathan Srebro, Jason Rennie, and Tommi Jaakkola. 2005. Maximum-Margin Matrix Factorization. In Advances in Neural Information Processing Systems, L. Saul, Y. Weiss, and L. Bottou (Eds.), Vol. 17. MIT Press. https://proceedings.neurips.cc/paper/2004/file/e0688d13958a19e087e123148555e4b4-Paper.pdf
- Quoc-Tuan Truong, Aghiles Salah, and Hady W. Lauw. 2021. Bilateral Variational Autoencoder for Collaborative Filtering. In Proceedings of the 14th ACM International Conference on Web Search and Data Mining (Virtual Event, Israel) (WSDM ’21). Association for Computing Machinery, New York, NY, USA, 292–300. https://doi.org/10.1145/3437963.3441759
- Yi Yang, Wei Qian, and Hui Zou. 2016. Insurance Premium Prediction via Gradient Tree-Boosted Tweedie Compound Poisson Models. arxiv:1508.06378 [stat.ME]
- Feng Yu, Qiang Liu, Shu Wu, Liang Wang, and Tieniu Tan. 2016. A dynamic recurrent model for next basket recommendation. In Proceedings of the 39th International ACM SIGIR conference on Research and Development in Information Retrieval. 729–732.
- Le Yu, Leilei Sun, Bowen Du, Chuanren Liu, Hui Xiong, and Weifeng Lv. 2020. Predicting Temporal Sets with Deep Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 1083–1091.
Permission to make digital or hard copies of part or all of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. Copyrights for third-party components of this work must be honored. For all other uses, contact the owner/author(s).
RecSys '21, September 27–October 01, 2021, Amsterdam, Netherlands
© 2021 Copyright held by the owner/author(s).
ACM ISBN 978-1-4503-8458-2/21/09.
DOI: https://doi.org/10.1145/3460231.3478844