StreamME: Simplify 3D Gaussian Avatar within Live Stream

Luchuan Song, University of Rochester, Rochester, New York, USA and Adobe Research, San Jose, California, USA, lsong11@ur.rochester.edu

Yang Zhou, Adobe Research, San Jose, California, USA, yazhou@adobe.com

Zhan Xu, Adobe Research, San Jose, California, USA, zhaxu@adobe.com

Yi Zhou, Adobe Research, San Jose, California, USA, yizho@adobe.com

Deepali Aneja, Adobe Research, San Jose, California, USA, aneja@adobe.com

Chenliang Xu, University of Rochester, Rochester, New York, USA, chenliang.xu@rochester.edu

DOI: https://doi.org/10.1145/3721238.3730635
SIGGRAPH Conference Papers '25: Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers, Vancouver, BC, Canada, August 2025

We propose StreamME, a method focuses on fast 3D avatar reconstruction. The StreamME synchronously records and reconstructs a head avatar from live video streams without any pre-cached data, enabling seamless integration of the reconstructed appearance into downstream applications. This exceptionally fast training strategy, which we refer to as on-the-fly training, is central to our approach. Our method is built upon 3D Gaussian Splatting (3DGS), eliminating the reliance on MLPs in deformable 3DGS and relying solely on geometry, which significantly improves the adaptation speed to facial expression. To further ensure high efficiency in on-the-fly training, we introduced a simplification strategy based on primary points, which distributes the point clouds more sparsely across the facial surface, optimizing points number while maintaining rendering quality. Leveraging the on-the-fly training capabilities, our method protects the facial privacy and reduces communication bandwidth in VR system or online conference. Additionally, it can be directly applied to downstream application such as animation, toonify, and relighting. Please refer to our project page for more details: https://songluchuan.github.io/StreamME/.

CCS Concepts: • Computing methodologies → Motion processing; • Computing methodologies → Animation; Motion processing;

Keywords: On-the-fly Training, 3D Gaussian Splatting, Point-Clouds Simplification

ACM Reference Format:
Luchuan Song, Yang Zhou, Zhan Xu, Yi Zhou, Deepali Aneja, and Chenliang Xu. 2025. StreamME: Simplify 3D Gaussian Avatar within Live Stream. In Special Interest Group on Computer Graphics and Interactive Techniques Conference Conference Papers (SIGGRAPH Conference Papers '25), August 10--14, 2025, Vancouver, BC, Canada. ACM, New York, NY, USA, 10 Pages. https://doi.org/10.1145/3721238.3730635

Fig. 1: The **StreamME** takes live stream (or monocular) video as input to enable rapid 3D head avatar reconstruction. It achieves impressive speed, capturing the basic facial appearance within 10 seconds (PSNR = 21 dB) and reaching high-quality fidelity (PSNR = 26 dB) within 5 minutes, as shown in (a). Notably, StreamME reconstructs facial features through on-the-fly training, allowing simultaneous recording and modeling without the need for pre-cached data (*e.g.* pre-training model). Additionally, StreamME facilitates real-time animation in (b), toonify in (c) and relighting in (d) (the background light image is shown in bottom right and we move the light position to create shadows on face) from the 5-minute reconstructed appearance, supporting the applications in VR and online conference. Natural face©*Xuan Gao et al.* (CC BY), and ©*Wojciech Zielonka et al.* (CC BY).

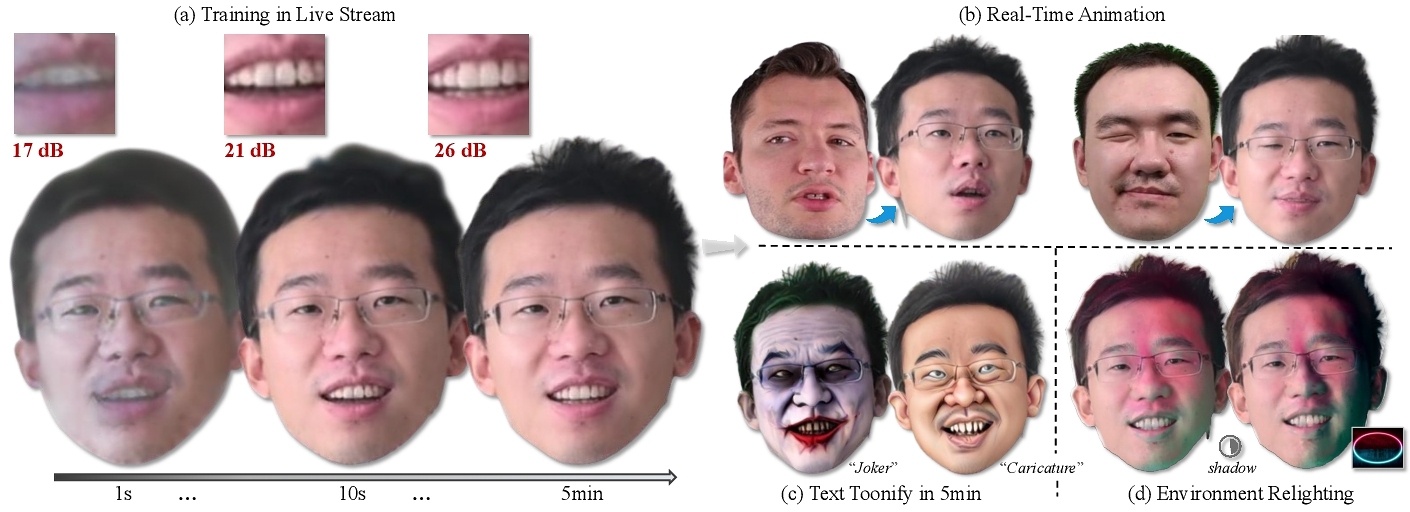
1 Introduction

The rapid reconstruction of head avatars reconstruction and reenactment of facial expression dynamics from a single video have become a rapidly advancing research tpoic, with vast potential for applications in VR/AR, digital human development, holographic communication, live streaming, and more. Recently, the volumetric models (e.g. Instance-NeRF [Liu et al. 2023] and 3DGS [Kerbl et al. 2023]) have endeavored to achieve both high-quality and efficient rendering. For instance, INSTA [Zielonka et al. 2022] employs Instant-NGP [Müller et al. 2022] to accelerate rendering through engineering optimizations. AvatarMAV [Xu et al. 2023] leverages the learnable blendshape as motion representation to achieve fast recovery of head avatar. FlashAvatar [Xiang et al. 2023] simulates the head avatar with a large number of Gaussian points in UV space. However, they continue to face challenges in balancing rendering quality and storage overhead, which constrains their applicability in consumer applications.

In this paper, we advance rapid facial reconstruction techniques to address the existing limitations. Additionally, we introduce a novel head avatar reconstruction task, termed on-the-fly training for reconstruction, which pushes the efficiency boundaries of fast reconstruction even further. Based on these observations, prior methods have uniformly separated training and inference processes due to efficiency constraints (refer as offline training). Such as, while AvatarMAV [Xu et al. 2023] achieves efficient training speeds offline, it cannot support frame-by-frame training for reconstruction within the live streaming. Our on-the-fly training approach offers multiple advantages, including (i) protect facial privacy by eliminating the need to pre-cached personal facial models on the external machines, (ii) only 3DGS parameters are transmitted in stream video, rather than the full images (about 70% compression) and (iii) the synchronous training and recording with real-time visualization, allowing for immediate re-recording of under-trained facial areas.

We propose a novel on-the-fly head avatar reconstruction method named StreamME. Different from the all previous head avatar reconstruction methods [Gao et al. 2024; Liu et al. 2024; Qian et al. 2023; Song et al. 2024a; 2021b; Wang et al. 2023b; Xiang et al. 2023; Xu et al. 2024; 2023; Zheng et al. 2022; 2023], the StreamME avoids dependence on multiple MLP layers to capture deformable facial dynamics (e.g., facial expression motion), significantly reducing expression recovery time and enabling true on-the-fly training. Specifically, we attach the 3D Gaussian point clouds to the tracked head mesh surface, allowing the points to move in tandem with mesh deformations. However, the point clouds associated with the deformed mesh on the 3D head template do not fully preserve the geometric properties of the face, which results in noise cloud artifacts around the rendered face and reducing the realism. From our method, we dynamically adjust the initial 3D Gaussian points through anchor-based pruning-and-clone strategy. Instead of selecting all points from the tracked head mesh as 3D Gaussian points, we identify specific anchor points that accurately capture facial motion. The 3D Gaussian points are then updated based on these selected anchors, optimizing for head representation. This strategy improves efficiency from eliminating points that do not contribute to facial motion, while preserving the motion anchor points critical for controlling facial deformation.

Meanwhile, we find in practice that more replicated 3D Gaussian points will lead to better quality but reduce speed, especially the training speed involving backpropagation. Therefore, we explored a method to gradually simplify the point clouds, which balance the number of point clouds and rendering quality. Here, we introduce two assumptions for simplifying point clouds: (i) the points should be distributed around the facial surface, rather than within it, as internal points remain unobservable due to occlusion; (ii) the small-size 3D Gaussian points with minimal volume, contribute negligibly to image quality and the impact is imperceptible. In optimization, these two assumptions serve as foundational principles. We ensure that 3D Gaussians are progressively distributed around and outside the surface, while occluded and small-sized points are removed, enhancing execution speed. This strategy yields a sparser 3D Gaussian representation of the head avatar, substantially improving efficiency without compromising rendering quality.

With the help of Motion-Aware Anchor Points selection and Gaussian Points Simplification strategy, we achieve on-the-fly photo-realistic head avatar representation within approximately 5 minutes of live streaming, as shown in Figure 1 (a). Moreover, the 3D Gaussian properties learned within 5 minutes can be applied to cross-identity head animation, facial toonification, environment relighting, and other applications with minimal fine-tuning, as illustrated in Figure 1 (b, c, d). This flexibility significantly broadens the application scope of our method. Furthermore, we demonstrate the superiority of our method through extensive experiments and comparisons with both instant and long-term training approaches. In summary, our contributions include the following aspects:

(1) We present the on-the-fly head avatar reconstruction method, which is able to reconstruct facial appearance from the live streams within about 5 minutes by pure Pytorch code. To the best of our knowledge, we are the first to reconstruct and visualize the head avatar within the on-the-fly training.

(2) We emphasize the efficiency in training, and introduce motion saliency anchor selection and point cloud simplification strategy. The anchor selection minimizes reliance on MLPs within the deformation field, while point cloud simplification strategy reduces computational redundancy from 3D Gaussian points.

(3) A series of downstream applications are attached, which have demonstrated the advances of our approach and provided novel insight for the on-the-fly training method.

Fig. 2: The overview the pipeline of **StreamME**. We list three components at here. i) The 3DGS Properties Warming-Up (Optional): we introduce two auxiliary learnable 3D Gaussian attribute texture and illumination, refining the UV vertex positions to improve facial geometry detail (*e.g.* here, we show the coarse displacement for the vertices around the hair). This step is optional, and the users may also opt to use the tracked head without displacement. ii) Anchor Duplication and Simplification: we freeze the Tex and SH attributes and introduce a binary learnable mask, initialized with all values set to 1, from the UV vertices sampled on the mesh. Natural face©*Xuan Gao et al.* (CC BY).

2 Related Works

2.1 Instant Head Avatar

The instant head avatar is an evolving field rooted in traditional photorealistic head reconstruction, and improved by novel techniques that reduce dependency on long-term training (e.g., StyleAvatar [Wang et al. 2023b], IM Avatar [Zheng et al. 2022], PointAvatar [Zheng et al. 2023], NeRFace [Gafni et al. 2021], KeypointNeRF [Mihajlovic et al. 2022] e.t.c) to achieve high-quality results. Recently, with the introduction of 3DGS [Kerbl et al. 2023] and NeRF acceleration [Müller et al. 2022] has driven rapid advancements in this field. The most notable works in this area include INSTA [Zielonka et al. 2023], AvatarMAV [Xu et al. 2023], and FlashAvatar [Xiang et al. 2023]. And the INSTA and FlashAvatar utilize mesh geometry sampling, with Instant-NGP and 3DGS employed for accelerated rendering, respectively. The AvatarMAV [Xu et al. 2023] employs blendshapes and uses the learnable MLPs to blend multiple implicit representations. Beyond these approaches, other head avatar reconstruction methods [Gafni et al. 2021; Wang et al. 2023b; Zheng et al. 2023] usually require several hours to several days to complete.

Additionally, the above methods utilize linearly decomposed facial expression parameters as coarse conditions, by neural convolution or MLP layers to refine the details such as hair and mouth details. In contrast to these approaches, we maintain high fidelity with more efficient in training and inference. With only the 3D Gaussian primitives attached to explicit geometry, we significantly reduce the learning burden from learnable neural networks and accelerate the training process. To our knowledge, this is the first work to achieve on-the-fly training for head avatar reconstruction.

2.2 Real-Time Face Estimation

The on-the-fly head avatar reconstruction depends on both efficient 3DGS training and real-time 3D head geometry estimation. As in previous works [Cao et al. 2022; Shao et al. 2024; Song et al. 2021a; 2024c; 2023; 2021c; Wang et al. 2022; Xiang et al. 2023; Xu et al. 2023], the preprocessed data is derived from estimating the pose and deformation of the facial template [Li et al. 2017] with tools such as MICA [MIC 2022]. It is highly time-consuming, for instance, processing a 10-minute video can require one day, which severely limiting its real-time applicability. In our case, we integrate a real-time face estimation (via [Li et al. 2017]) module to supply pose and head mesh data on-the-fly within the pipeline. Notably, we have meticulously designed the system to balance resource allocation across facial parsing, head tracking, and 3DGS reconstruction within the real-time pipeline.

2.3 Deformable-3DGS Representations

The 3D Gaussian Splatting (3DGS) [Kerbl et al. 2023] is designed to represent and render static 3D scenes. Building on static 3DGS, deformable-3DGS [Chen et al. 2024; Qian et al. 2024; Song et al. 2024b] incorporates MLPs or CNNs to predict and render geometric deformations, with 3D Gaussian properties predicted frame-by-frame over time. Specifically, these methods retain a canonical 3D Gaussian space, optimizing the MLP-based deformation field [Wang et al. 2023a; Zhang et al. 2023; 2024] conditioned on timestamps.

Our method also employs the canonical-to-world space strategy. First, the tracked deformed meshes are positioned within canonical space. Then, 3D Gaussian points are placed around the surface and transformed into world space, incorporating pose information for rendering. Additionally, our method eliminates the need for learnable layers to predict deformations, instead, the deformations are derived from 3D Gaussian points around the meshes which are deformed from canonical space.

Fig. 3: We employ the proposed **Idx** for anchor binding, elimination the motion irrelevant points and simplification the over-small size/opacity points to reduce computational overhead. Specifically, (a) The anchor points are sampled from the mesh and multiple duplicated for detail representation. (b) The motion-aware **Idx** tends to remove points, as there are none motion gradients around the forehead in canonical space. (c) The learnable masks from **Idx** for deleting the small size and opacity points within training. Please zoom-in for details. Natural face©*Xuan Gao et al.* (CC BY).

3 Method

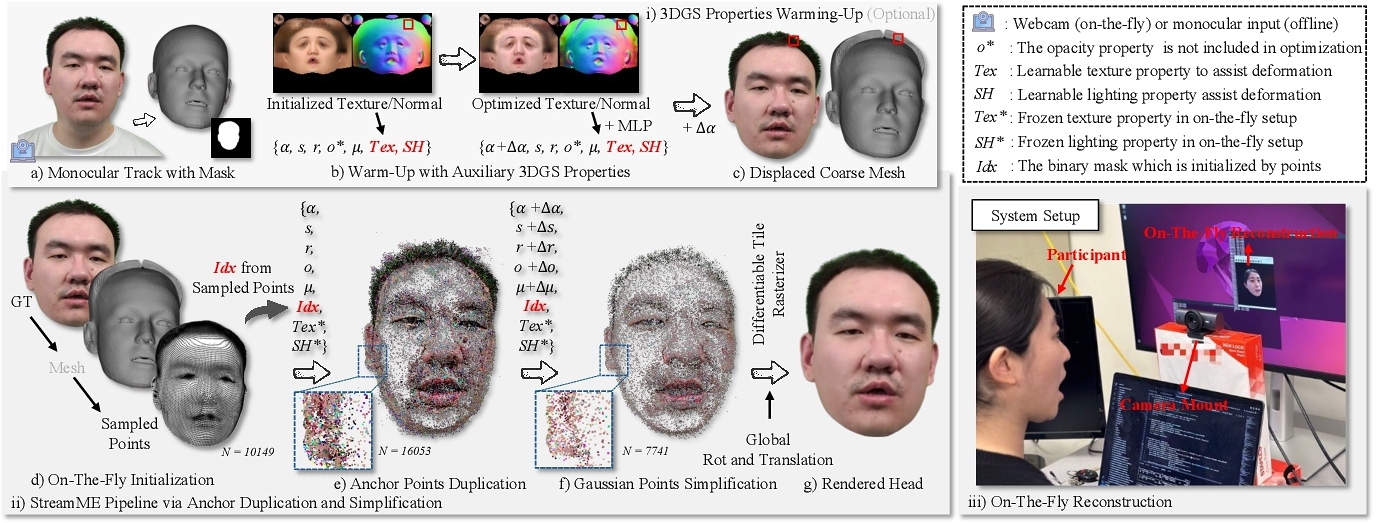
The StreamME generates the 3D head avatar within few minutes from streaming. And progressively simplifying the 3D Gaussian point representation of the face while retaining anchor points essential to capturing facial motion. In this section, we will introduce the simplification 3D Gaussians representation and the system pipeline, which is also shown in Figure 2.

3.1 Preliminaries

In our approach, we build upon the 3DGS [Kerbl et al. 2023], a point-based representation from 3D Gaussian properties for dynamic 3D head reconstruction. In 3DGS, a covariance matrix (Σ) and the mean of point (μ) are defined for each Gaussian g:

\begin{equation} g = e^{-\frac{1}{2}(\mathbf {x} -\mu)^T \Sigma ^{-1} (\mathbf {x} -\mu)}. \end{equation}
(1)

For differentiable optimization, the covariance matrix Σ is decomposed into a rotation matrix R and a scaling matrix S, parameterized by a learnable quaternion r and scaling vector s. For spatial attributes, the 3D Gaussians possess the color of the projected pixels are from the splatting and overlapping of the 3D Gaussians points:

\begin{equation} \mathbf {C} = \sum _{i \in N} \mathbf {c}_i \alpha _i \prod _{j=1}^{N-1} (1-\alpha _j). \end{equation}
(2)

Here, α_i represents the density derived from the projection of 3D Gaussians with Σ and opacity o, and N denotes the number of points. Consequently, we define the 3D Gaussian attributes as follows:

\begin{equation} g = \lbrace \alpha, s, r, o, \mu \rbrace. \end{equation}
(3)

The attributes are optimized in backpropagation rendering pipeline. Generally, Gaussian properties derived from precise geometry result in higher rendering quality.

3.2 Gaussian Properties Warm-up

Inspired by previous works [Qian et al. 2023; Xu et al. 2024], we adjust vertices in the tracked coarse head geometry to account for deformations caused by features like hair, the standard facial templates fall short in representing the full head shape. However, the preprocessing step in those method (e.g. DMTet [Shen et al. 2021] or VHAP [Qian 2024]) require substantial time to reorient the geometry and frequently suffer from collapse due to the limitations of single or sparse views.

We propose a warm-up step that introduces additional learnable texture (Tex) and illumination (SH) parameters to assist vertex deformation via 3DGS, achieving reorientation within 20 seconds. Specifically, we follow FlashAvatar [Xiang et al. 2023] to initialize the 3D Gaussian points from UV coordinates. Then, the vertex positions are learned in 3D Gaussian properties α. We apply the learnable texture with illumination to the diffuse color features of each 3D Gaussian point and the normal consistency between adjacent faces on a mesh surface to keep the smoothness, as shown in Figure 2. It is worth noting that this explicit geometric deformation step is optional and could be skipped to improve the operation efficiency. Furthermore, the auxiliary learnable parameters Math 4 and Math 5 are optimized only during the warm-up step and remain frozen in subsequent stages. In practice, we set the static Direct-Current component (the self.feature_dc) in 3DGS as the Math 6 .

3.3 Motion-Aware Anchor Points

Our primary optimization strategy for 3D Gaussians involves gradually removing points irrelevant to facial motion and duplicating those that contribute significantly (termed as anchor points), as shown in Figure 3 (a). For static scene or object reconstruction, the gradient accumulation of each 3D Gaussians position in the optimizer serves as the basis for duplication and pruning. However, this point cloud optimization method is not suitable for our task, as the regions around the eyes and teeth is dynamic.

Meanwhile, we initialize a learnable binary auxiliary Gaussian attribute from the UV vertices, named as Idx ∈ {0, 1}^N (N is the number of points), as shown in Figure 2. The accumulation of density gradients does not only come from the optimized gradients but also from positional differences relative to the normalized canonical point cloud. In practice, we apply the canonical point cloud ($\bar{{\bf P}}_0$) of the face in the first frame as the normalized reference. Then for each Gaussian point, we calculate the gradient as the following:

\begin{equation} \mathit {\mathbf {Idx}} = \left\lbrace \begin{aligned} 1 &, & < \alpha _{grad}, \nabla \mathbf {P}> _{\text{max}} \ge \epsilon, \\ 0 &, & < \alpha _{grad}, \nabla \mathbf {P}> _{\text{max}} < \epsilon. \end{aligned} \right. \end{equation}
(4)

Here, ϵ represents the threshold for the maximum between optimizer and motion gradient, the ∇P is the accumulated gradient of P relative to $\bar{{\bf P}}_0$ (first-order difference). Points with a value of 1 in Idx will be cloned, while those with a value of 0 will be pruned. The α_grad is the gradient of density.

This approach retains points that contribute to facial motion while eliminating those do not, as in Figure 3 (b). These motion anchors effectively control the proliferation of non-contributory points and adapt swiftly to facial expression changes without requiring additional neural networks (e.g., MLPs or CNNs) for fitting facial motion via expression. However, due to duplication, the excessive density around the anchor points leads to additional computational overhead as the anchor points and their duplicates proliferate exponentially.

3.4 Gaussian Points Simplification

To regulate the over-proliferation of Gaussian anchor points, the basic strategy periodically reduces opacity values, removing points that consistently remain at low opacity levels. However, this opacity-based control method is effective in static scene reconstruction, but it conflicts with our method. Generally, points that are fully transparent (with opacity 0) typically do not contribute to motion, such as those located on the forehead around the head. Then, we propose two methods for optimizing the number of these points, removing excessively small points and aligning remaining points closer to geometric surface. Points positioned closer to surface better represent details, while those farther away tend to introduce noise.

We apply the learnable binary index Idx as the mask on the opacity property o and scale property s (updated to o′, s′), as:

(5)

which means that those Gaussian points with motion gradient contributions (Idx value with 1) are additionally applied on the scale and opacity. Then, we adopt the straight-through estimator [Bengio et al. 2013] for gradient calculation with binary parameters, as the following:

\begin{equation} \begin{aligned} \mathbf {Idx}^{\prime } = \text{sigm}(\mathbf {Idx}) + \text{sg}[\mathbb {U}[\text{sigm}({\mathbf {Idx}}) > \epsilon ^{\prime }] - \text{sigm}(\mathbf {Idx})], \end{aligned} \end{equation}
(6)

where the sigm, sg, $\mathbb {U}$ are the sigmoid function, stop gradients and indicator function (mapping with 0 and 1). The ϵ′ are the pre-defined threshold, which is set to 0.01. During forward-propagation, the mask applied on o and s via the value of Idx. In back-propagation, gradients are obtained from the derivative of sigm(Idx), which solves the non-differentiability of binarization. It is shown in Figure 3 (c), the redundant points are eliminated.

Meanwhile, we propose a point-to-surface measurement to reduce the proliferation of points located far from the face, as these points contribute little yet significantly increase computational cost. Specifically, the projected distance of each point to the initialization surface is calculated, and the positions of discrete points and their corresponding surface points are indexed by the the anchor points and point clusters bound by the anchor points in:

\begin{equation} \begin{aligned} d = \sum _{A \in \mathbf {Idx}} \mathbf {Idx} \cdot \sum _{\mathbf {P}\in A} ||(\mathbf {P}-\mathbf {P}_0^A)\cdot n_0^A||, \end{aligned} \end{equation}
(7)

where $n_0^A$ is unit normal of anchor points $\mathbf {P}_0^A$, and P is the bound points with anchor $\mathbf {P}_0^A$, then we find the anchor points through Idx. The regularization on d will make the bound points around the anchor point closer to the corresponding position on the surface, and minimizing the offset.

4 Experiments

4.1 Implementation Details

4.1.1 Datasets. We perform experiments with 6 subjects monocular videos from the public datasets GaussianBlendshape [Ma et al. 2024], NeRFBlendshape [Gao et al. 2022], StyleAvatar [Wang et al. 2023b], and InstantAvatar [Zielonka et al. 2023] in the offline training setup. Moreover, we apply self-captured video via webcam within on-the-fly training. The online/offline experiments are presented with the resolution of 512 × 512. In offline setup, we take an average length of 1000-5000 frames for training (about 80%) while the test dataset includes frames with novel expressions and poses (about 20%), which is aligned with baseline methods. The sequential/random inputs are applied for online/offline set-up, respectively. For each frame, the RobustVideoMatting [Lin et al. 2022] is used to remove background.

4.1.2 Hyperparameters. The 3D Gaussian points are initialized with learning rates for Gaussian properties {α, s, r, o, μ, Idx} set to {1e^{− 5}, 5e^{− 3}, 1e^{− 3}, 5e^{− 2}, 2.5e^{− 3}, 1e^{− 4}}. During pre-training, the learning rates for auxiliary properties {Tex, SH} are {2e^{− 4}, 1e^{− 4}}, while the others remain the same. The threshold of α_grad and ∇P is set to 0.01. The α_grad is computed by the accumulated gradient of α (the self.xyz_gradient_accum in 3DGS). For the online optimization, we construct each mini-batch with multiple images, comprising one newly captured frame and several previously captured frames, to mitigate forgetting of historical information.

4.1.3 Losses. We apply L₁ and SSIM in training. Meanwhile, the distance between the points and surface in Eq. 7 as regularization. For warm-up phrase, we introduce dark channel loss to separate the learnable Tex and SH coefficients. During training, the weights for the L₁ and SSIM losses are set to 1 and 0.1, respectively, with a regularization term weight of 0.01. Additionally, a dark channel loss with the weight of 10 is incorporated for the warm-up phrase.

4.1.4 Pipeline Details. We set the head geometry corresponding to the initial frame as canonical points clouds, and the position difference of the subsequent point clouds relative to the canonical point cloud is used as the motion gradient. The motion gradients are also cloned with the anchor points and deleted with non-contributing points. We achieve that by introducing learnable parameters Idx. The points with Idx value corresponds to 0 are deleted, and the points with value as 1 are cloned. We allocate approximately 30 seconds for the warm-up phase within on-the-fly pipeline (a longer warm-up duration is not recommended, as it may cause collapse). We execute the cloning/pruning every 1500 optimization iterations.

Fig. 4: The perceptual evaluation of our method and baselines for self-reenactment. Baseline methods are evaluated with their default settings, and time consumption is recorded under the official provided iteration. Blue arrows on the ground-truth highlight regions of interest for closer inspection. Please zoom in for detailed comparison. Natural face©*Lizhen Wang et al.* (CC BY), and ©*Wojciech Zielonka et al.* (CC BY).

4.2 Baseline

Given the challenges associated with high-efficient avatar reconstruction, especially completing reconstruction within minutes while achieving re-animation, few methods exactly handle this task. Therefore, we select several related works for comparison, as,

AvatarMAV [Xu et al. 2023]: This method applies a NeRF-based implicit neural blend representation. By training a lightweight-MLP, it integrates multiple learnable implicit neural shapes for appearance. It claims to accomplish head reconstruction in 5 minutes (256 × 256 resolution). Here, the resolution is reset to 512 × 512 to align with baselines.
FlashAvatar [Xiang et al. 2023]: The FlashAvatar builds on 3DGS, utilizing UV sampling for Gaussian initialization and an offset network with MLPs to dynamically model variations in facial expressions. It reports inference speed but omits the time required for reconstruction.
GaussianBlendshape [Ma et al. 2024]: It is the state-of-the-art in monocular reconstruction based on 3DGS. This approach models facial motion through the mixture of explicitly learnable blendshapes aligned with the pre-tracked FLAME expression coefficients.

The FlashAvatar and GaussianBlendshape are from the preprocessed FLAME via MICA [MIC 2022], which is time-intensive and unsuitable for on-the-fly reconstitution. We also acknowledge other related methods, such as NeRFBlendshape [Gao et al. 2022], HeadGaS [Dhamo et al. 2024] and MonoGaussianAvatar [Chen et al. 2024] etc. However, we exclude these methods from comparison due to their on-the-fly reconstruction setups and comparable performance (e.g., INSTA [Zielonka et al. 2023] and AvatarMAV employ fast training by sampling rays from NeRF [Mildenhall et al. 2020], yet exhibit slow inference when releasing all rays).

4.3 Numerical Results and Comparisons

We take two criteria for numerical evaluations, one is from quantitative measurement, the other is from human assessment.

4.3.1 Quantitative Metrics. It is based on three aspects. (1) Image Quality: We use the PSNR, LPIPS [Zhang et al. 2018] and MSE for the evaluation of self-reenactment image quality. (2) Inference Frame Rate: The inference frame rate (FPS) the measurement of the number of frames generated within per second without introducing the head tracking, which is not the speed of the pipeline. It is measured on a single NVIDIA RTX4090 GPU. (3) Memory Storage: The memory storage (Mem.) is the storage capacity occupied by the models, the compact models offer advantages in both computational efficiency and storage requirements. We use the Megabyte (MB) as units. The quantitative experiments are performed on the self-reenactment.

4.3.2 User Study. We sample 6 distinct identities, each represented by 20 video clips (5 for self-reenactment and 15 for cross-reenactment), and invite 30 participants for the human evaluation. The Mean Opinion Scores (MOS) rating protocol is employed, with participants asked to assess the generated videos across four criteria: (1) MS (Motion Synchronization): To what extent do you agree that the head motion in the animated videos is synchronized with the driving source? and (2) VQ (Video Quality): To what extent do you agree that the overall video quality is high, considering factors such as frame quality, temporal consistency, and so forth? A 5-point Likert scale is used for each criterion, with scores ranging from 1 to 5, where 1 represents "strongly disagree" and 5 represents "strongly agree" (higher scores indicate better performance).

Fig. 5: The perceptual evaluation of our method and baselines for cross-reenactment. Our method demonstrates superior preservation of high-frequency facial details, including features such as teeth and hair. Please zoom in for a closer view. Natural face©*Lizhen Wang et al.* (CC BY), ©*Xuan Gao et al.* (CC BY) and ©*Wojciech Zielonka et al.* (CC BY).

Table 1: (1) Left part: Quantitative evaluation results compared with baseline methods. The best scores are highlighted in bold, with the second-best underlined. Symbols ↓ and ↑ denote whether lower or higher values indicate superior performance, respectively. All experiments were conducted on a single NVIDIA RTX4090 machine. (2) Right part: A 5-point Likert scale is used for the user study, where scores closer to 5 signify better performance.

Methods	PSNR↑	MSE↓	LPIPS↓	FPS↑	Mem.↓	MS↑	VQ↑
	dB	→ 0	→ 0		MB	→ 5
	Quantitative Results					User Study
AvatarMAV	24.1	0.047	0.137	2.58	14.1	3.1	2.3
FlashAvatar	27.8	0.021	0.109	94.5	12.6	3.8	3.1
GaussianBlendshape	26.4	0.017	0.112	22.9	872	3.7	3.6
StreamME	29.7	0.012	0.095	139	2.52	3.9	4.1

4.4 Quality Comparison with Baseline Methods

The quality comparison results of self-reenactment are shown in Table 1 and Figure 4 respectively. From Table 1, our method achieves the best results in user study and quantitative evaluations. The FlashAvatar is a powerful baseline, but still requires a lot of time to train the learnable MLP layers. The AvatarMAV is fast but exhibits limited detail preservation at 512 × 512 resolution.

The perceptual comparisons for cross-reenactment are illustrated in Figure 5, where our method consistently delivers superior results. The AvatarMAV and FlashAvatar exhibit noticeable artifacts on out-of-distribution expressions, as their learnable MLP layers struggle to adapt to expression changes within few iterations (for efficiency). GaussianBlendshape, on the other hand, underperforms due to the lack of conditions aligned with blendshapes during training. Our approach circumvents the need for MLPs and blendshapes as training conditions by directly binding appearance representations to the point cloud, enabling efficient training while preserving high quality across diverse facial expressions.

Table 2: The quantitative results of image quality and number of iterations (Iters.) at each time point. The Iters. represents the training iteration speed in the same unit time, a higher value indicates better training efficiency. Our method achieves comparable quality in just two minutes, whereas other methods require 30 minutes to reach the same standard.

Methods	PSNR	Iters.	PSNR	Iters.	PSNR	Iters.	PSNR	Iters.
	Time = 1s		Time = 10s		Time = 2min		Time = 30in
AvatarMAV	3.12	7.6e¹	21.7	7.9e²	24.1	9.6e³	24.4	1.4e⁵
FlashAvatar	4.90	9.7e¹	12.5	9.4e²	16.9	1.2e⁴	26.8	1.7e⁵
GaussianBlendshape	7.29	2.9e¹	15.6	3.7e²	25.2	4.8e³	25.8	6.1e⁴
StreamME	10.8	1.4e²	23.1	1.5e³	27.2	1.6e⁴	29.8	3.4e⁵

4.5 Efficiency Comparison with Baseline Methods

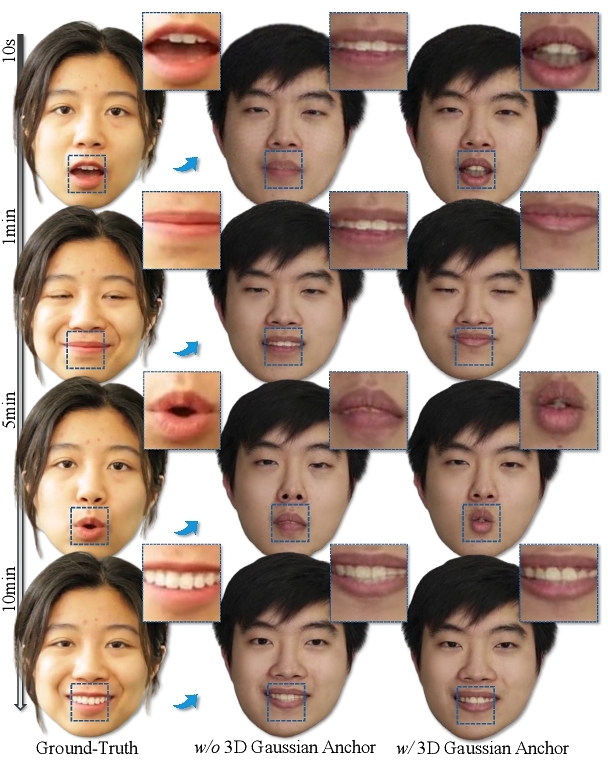
In addition to quality comparisons, we further validate the efficiency improvements achieved by our method. Specifically, we evaluate the models at various training stages (iterations and time) on testset. The model capacity at each training slot will be examined for comparison. The results are shown in Figure 6 and Table 2, it can be found that compared with the baseline method, our approach achieves convergence within 2 minutes, and simulates dynamic expression from the outset. As shown in Figure 6, our method synthesizes detailed tooth within just 10 seconds and simulates dynamic expressions without any warm-up phase. The efficiency is due to it is geometric foundation, avoiding reliance on learnable MLPs. Additionally, as shown in the Table 2, different from the nearly constant training speed of baseline methods, our method improves training efficiency over time due to the progressively sparse point clouds, which reduce computational redundancy.

Fig. 6: The visualization of efficiency comparison with baseline methods, with results recorded from 1 second until the point at which all methods achieve convergence (about 30 minutes). Please zoom in to compare the fine details of teeth, eyes, hair, and the subtle differences in facial expressions. It is noteworthy that our method is able to achieve the representation of expressions and details with few iterations and time consumption. Natural face ©*Wojciech Zielonka et al.* (CC BY).

4.6 Ablation Study

Fig. 7: The visualize of ablation study on Gaussian properties warm-up phrase. Here, the explicit geometric deformation serves the same function as the deform MLP during the 3DGS training phase. For results without the deform MLP, those initialized with accurate geometric deformation from the warm-up phase show improved quality over those initialized from the template head, particularly in outer facial regions like the hair via red arrow, as seen in the second column (left to right). However, introducing the MLP in 3DGS training compensates effectively for this difference, as illustrated in the third column (left to right), since both approaches focus on adjusting point positions. Natural face©*Luchuan Song et al.* (CC BY).

Fig. 8: The warm-up phase helps geometry adjustment for 3D Gaussian initialization. We showcase its head geometry simulation from multiple viewpoints, highlighting the consistent of hair geometry. The vertex offset obtained could subsequently be applied to improve the head tracking. Natural face©*Wojciech Zielonka et al.* (CC BY).

Fig. 9: The visualize of image quality via 3D Gaussian anchor. With the 3D Gaussian anchor, the model instantly adapts to dynamic expressions. Natural face©*Yufeng Zheng et al.* (CC BY) and ©*Lizhen Wang et al.* (CC BY).

Fig. 10: The visualize of points cloud via 3D Gaussian anchor and simplification. The point cloud is filtered to eliminate points with low contributions to motion. This simplification further optimizes the number of point clouds. As shown by the detailed representation of hair, the optimized point clouds preserve high-frequency features. Natural face©*Yufeng Zheng et al.* (CC BY).

In this section, we present ablation studies on Gaussian properties warm-up, Gaussian motion anchors, and Gaussian simplification to validate the importance of these modules.

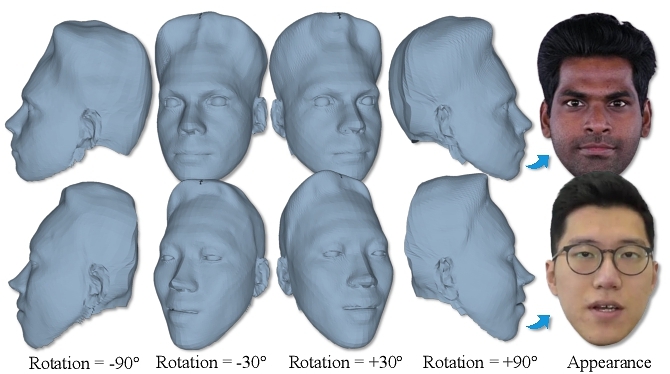
4.6.1 Ablation study on Gaussian properties warm-up. We present the improvement provided by the 3D Gaussian properties warm-up. As illustrated in Figure 2, we label it as optional since it functions equivalently to the point cloud deformation MLP. Specifically, it pre-simulates the point cloud offset of the 3D head template, providing prior positional information for the 3D Gaussians. To conduct the ablation study, we introduce the position offset MLP (delta MLP) with (w/) and without (w/o) warm-up intervention, as shown in Figure 7. In the results without the delta MLP, warm-up contributes to clearer details in out-of-face areas, such as hair. Incorporating the MLP mitigates this issue, improving the detail clarity, while slightly reduce execution efficiency.

At the same time, the properties warm-up will provide head geometry, which only takes about 10 seconds and several appearances from different perspectives for fitting, as shown in Figure 8, which is much faster than head fitting algorithms such as VHAP [Qian 2024] and MonoNPHM [Giebenhain et al. 2024]. Although its geometric accuracy could be further enhanced, it strikes a balance between geometry and 3D Gaussian feature representation.

Fig. 11: The visualize of the 3D Gaussian simplification. We present the rendered appearance and MSE pixel error maps corresponding to with (w/) and without(*w/o*) simplification at different time slots. The mean error values are in the upper right corner of each error map. As the first pruning does not occur at 0 sec, we begin recording from the 30th second. The introduction of simplification will not result in any reduction in qualitative and quantitative results, but lead to a significant improvement in efficiency. Natural face©*Luchuan Song et al.* (CC BY).

Fig. 12: Comparisons in the ablation study on w/ and *w/o* 3D Gaussian simplification. For *w/o* simplification, as the number of iterations grows, the time per iteration also increases due to the overhead from redundant points. In contrast, simplified pruning (w/ simplification) enables the system to maintain high efficiency throughout. The FPS represents the training iterations per second. The corresponding number of 3D Gaussian points are annotated for reference. And the dark gray region indicates that w/ simplification has converged.

4.6.2 Ablation study on motion-aware anchor. The motion-aware anchor selection leverages the motion gradient prior, progressively duplicating points associated with motion. This approach enables dynamic facial expressions to be directly mapped onto geometric structures, bypassing the need for extensive iterative training steps for adaptation. As shown in Figure 9, the motion-aware anchor efficiently adapts to dynamic facial expressions at the beginning of training, whereas without it, a warp-up period of approximately 10 minutes would be required. Additionally, it optimizes the number of point clouds by incorporating motion gradients, and eliminates the points unrelated to facial movement, as illustrated in Figure 10.

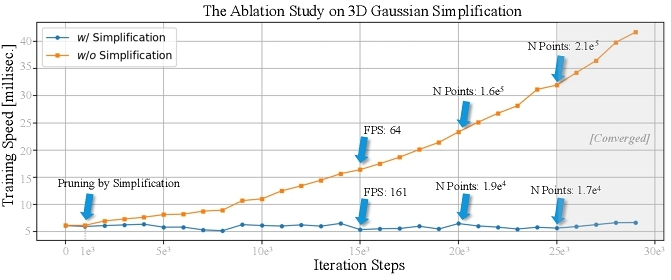
4.6.3 Ablation study on 3D Gaussian simplification. The simplification of 3D Gaussian points is designed to reduce computational load without sacrificing rendering quality, as shown in Figure 10 (w/ Simplification). Although denser point clouds are generally associated with higher detail, in our case, redundant points contribute minimally to 3DGS. Figure 11 presents the comparison of results with (w/) and without (w/o) simplification. As shown, point cloud simplification does not result in a decrease in quality, as confirmed by the error maps and mean error values. Specially, after more than 10 minutes of training (about 1e⁵ iterations), w/ simplification achieves approximately 8 − 10 times the reduction of points number compared to w/o simplification (the numbers are from 200k to 24k), which has a significant improvement in efficiency. Additionally, the quantitative comparison results are shown in the Figure 12, the method with simplification (w/ simplification) maintains high efficiency throughout the training phase. Moreover, the average number of point clouds for training subjects after convergence is 9,807, compared to 13,453 for FlashAvatar and 62,530 for GaussianBlendshape, which demonstrates the cloning and pruning effectively reduce the number of points.

5 Discussion and Conclusion

We present StreamME, a on-the-fly head avatar training (or reconstruction) method from monocular live stream. It analyzes the number of point clouds in the 3D Gaussian field, evaluates the points distribution to achieve a more optimal arrangement over explicit face geometry, and removes points with lower contributions on scale and opacity to reduce computational complexity. The designs help our method achieves a diversity of facial expressions solely through geometry without dependence on the learnable MLPs, which significantly improves training speed. Furthermore, a series of applications (e.g. toonification and relighting) have been developed based on our method, which bringing more exploration directions in the future.

References

2022. Towards Metrical Reconstruction of Human Faces.
Yoshua Bengio, Nicholas Léonard, and Aaron Courville. 2013. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv preprint arXiv:1308.3432 (2013).
Chen Cao, Tomas Simon, Jin Kyu Kim, Gabe Schwartz, Michael Zollhoefer, Shun-Suke Saito, Stephen Lombardi, Shih-En Wei, Danielle Belko, Shoou-I Yu, et al. 2022. Authentic volumetric avatars from a phone scan. ACM Transactions on Graphics (TOG) 41, 4 (2022), 1–19.
Yufan Chen, Lizhen Wang, Qijing Li, Hongjiang Xiao, Shengping Zhang, Hongxun Yao, and Yebin Liu. 2024. Monogaussianavatar: Monocular gaussian point-based head avatar. In ACM SIGGRAPH 2024 Conference Papers. 1–9.
Helisa Dhamo, Yinyu Nie, Arthur Moreau, Jifei Song, Richard Shaw, Yiren Zhou, and Eduardo Pérez-Pellitero. 2024. Headgas: Real-time animatable head avatars via 3d gaussian splatting. In European Conference on Computer Vision. Springer, 459–476.
Guy Gafni, Justus Thies, Michael Zollhöfer, and Matthias Nießner. 2021. Dynamic Neural Radiance Fields for Monocular 4D Facial Avatar Reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). 8649–8658.
Xuan Gao, Haiyao Xiao, Chenglai Zhong, Shimin Hu, Yudong Guo, and Juyong Zhang. 2024. Portrait Video Editing Empowered by Multimodal Generative Priors. arXiv preprint arXiv:2409.13591 (2024).
Xuan Gao, Chenglai Zhong, Jun Xiang, Yang Hong, Yudong Guo, and Juyong Zhang. 2022. Reconstructing Personalized Semantic Facial NeRF Models From Monocular Video. ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia) 41, 6 (2022). https://doi.org/10.1145/3550454.3555501
Simon Giebenhain, Tobias Kirschstein, Markos Georgopoulos, Martin Rünz, Lourdes Agapito, and Matthias Nießner. 2024. MonoNPHM: Dynamic Head Reconstruction from Monocular Videos. In Proc. IEEE Conf. on Computer Vision and Pattern Recognition (CVPR).
Bernhard Kerbl, Georgios Kopanas, Thomas Leimkühler, and George Drettakis. 2023. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Transactions on Graphics 42, 4 (2023).
Tianye Li, Timo Bolkart, Michael. J. Black, Hao Li, and Javier Romero. 2017. Learning a model of facial shape and expression from 4D scans. ACM Transactions on Graphics, (Proc. SIGGRAPH Asia) 36, 6 (2017), 194:1–194:17. https://doi.org/10.1145/3130800.3130813
Shanchuan Lin, Linjie Yang, Imran Saleemi, and Soumyadip Sengupta. 2022. Robust high-resolution video matting with temporal guidance. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision. 238–247.
Pinxin Liu, Luchuan Song, Daoan Zhang, Hang Hua, Yunlong Tang, Huaijin Tu, Jiebo Luo, and Chenliang Xu. 2024. Emo-avatar: Efficient monocular video style avatar through texture rendering. arXiv e-prints (2024), arXiv–2402.
Yichen Liu, Benran Hu, Junkai Huang, Yu-Wing Tai, and Chi-Keung Tang. 2023. Instance neural radiance field. In Proceedings of the IEEE/CVF International Conference on Computer Vision. 787–796.
Shengjie Ma, Yanlin Weng, Tianjia Shao, and Kun Zhou. 2024. 3D Gaussian Blendshapes for Head Avatar Animation. arXiv preprint arXiv:2404.19398 (2024).
Marko Mihajlovic, Aayush Bansal, Michael Zollhoefer, Siyu Tang, and Shunsuke Saito. 2022. KeypointNeRF: Generalizing image-based volumetric avatars using relative spatial encoding of keypoints. In European conference on computer vision. Springer, 179–197.
Ben Mildenhall, Pratul P Srinivasan, Matthew Tancik, Jonathan T Barron, Ravi Ramamoorthi, and Ren Ng. 2020. NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part I. 405–421.
Thomas Müller, Alex Evans, Christoph Schied, and Alexander Keller. 2022. Instant neural graphics primitives with a multiresolution hash encoding. arXiv preprint arXiv:2201.05989 (2022).
Shenhan Qian. 2024. Versatile Head Alignment with Adaptive Appearance Priors. (September 2024). https://github.com/ShenhanQian/VHAP
Shenhan Qian, Tobias Kirschstein, Liam Schoneveld, Davide Davoli, Simon Giebenhain, and Matthias Nießner. 2023. GaussianAvatars: Photorealistic Head Avatars with Rigged 3D Gaussians. arXiv preprint arXiv:2312.02069 (2023).
Zhiyin Qian, Shaofei Wang, Marko Mihajlovic, Andreas Geiger, and Siyu Tang. 2024. 3dgs-avatar: Animatable avatars via deformable 3d gaussian splatting. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 5020–5030.
Zhijing Shao, Zhaolong Wang, Zhuang Li, Duotun Wang, Xiangru Lin, Yu Zhang, Mingming Fan, and Zeyu Wang. 2024. Splattingavatar: Realistic real-time human avatars with mesh-embedded gaussian splatting. arXiv preprint arXiv:2403.05087 (2024).
Tianchang Shen, Jun Gao, Kangxue Yin, Ming-Yu Liu, and Sanja Fidler. 2021. Deep marching tetrahedra: a hybrid representation for high-resolution 3d shape synthesis. Advances in Neural Information Processing Systems 34 (2021), 6087–6101.
Luchuan Song, Lele Chen, Celong Liu, Pinxin Liu, and Chenliang Xu. 2024a. TextToon: Real-Time Text Toonify Head Avatar from Single Video. arXiv preprint arXiv:2410.07160 (2024).
Luchuan Song, Bin Liu, Guojun Yin, Xiaoyi Dong, Yufei Zhang, and Jia-Xuan Bai. 2021b. Tacr-net: editing on deep video and voice portraits. In Proceedings of the 29th ACM International Conference on Multimedia. 478–486.
Luchuan Song, Bin Liu, and Nenghai Yu. 2021a. Talking face video generation with editable expression. In Image and Graphics: 11th International Conference, ICIG 2021, Haikou, China, August 6–8, 2021, Proceedings, Part III 11. Springer, 753–764.
Luchuan Song, Pinxin Liu, Lele Chen, Guojun Yin, and Chenliang Xu. 2024b. Tri 2-plane: Thinking Head Avatar via Feature Pyramid. In European Conference on Computer Vision. Springer, 1–20.
Luchuan Song, Pinxin Liu, Guojun Yin, and Chenliang Xu. 2024c. Adaptive Super Resolution for One-Shot Talking Head Generation. IEEE International Conference on Acoustics, Speech, and Signal Processing.
Luchuan Song, Guojun Yin, Zhenchao Jin, Xiaoyi Dong, and Chenliang Xu. 2023. Emotional listener portrait: Realistic listener motion simulation in conversation. In 2023 IEEE/CVF International Conference on Computer Vision (ICCV). IEEE, 20782–20792.
Luchuan Song, Guojun Yin, Bin Liu, Yuhui Zhang, and Nenghai Yu. 2021c. Fsft-net: face transfer video generation with few-shot views. In 2021 IEEE International Conference on Image Processing (ICIP). IEEE, 3582–3586.
Can Wang, Ruixiang Jiang, Menglei Chai, Mingming He, Dongdong Chen, and Jing Liao. 2023a. Nerf-art: Text-driven neural radiance fields stylization. IEEE Transactions on Visualization and Computer Graphics (2023).
Lizhen Wang, Xiaochen Zhao, Jingxiang Sun, Yuxiang Zhang, Hongwen Zhang, Tao Yu, and Yebin Liu. 2023b. StyleAvatar: Real-time Photo-realistic Portrait Avatar from a Single Video. arXiv preprint arXiv:2305.00942 (2023).
Ziyan Wang, Giljoo Nam, Tuur Stuyck, Stephen Lombardi, Michael Zollhöfer, Jessica Hodgins, and Christoph Lassner. 2022. Hvh: Learning a hybrid neural volumetric representation for dynamic hair performance capture. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 6143–6154.
Jun Xiang, Xuan Gao, Yudong Guo, and Juyong Zhang. 2023. FlashAvatar: High-Fidelity Digital Avatar Rendering at 300FPS. arXiv preprint arXiv:2312.02214 (2023).
Yuelang Xu, Benwang Chen, Zhe Li, Hongwen Zhang, Lizhen Wang, Zerong Zheng, and Yebin Liu. 2024. Gaussian Head Avatar: Ultra High-fidelity Head Avatar via Dynamic Gaussians. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR).
Yuelang Xu, Lizhen Wang, Xiaochen Zhao, Hongwen Zhang, and Yebin Liu. 2023. AvatarMAV: Fast 3D Head Avatar Reconstruction Using Motion-Aware Neural Voxels. In ACM SIGGRAPH 2023 Conference Proceedings.
Junzhe Zhang, Yushi Lan, Shuai Yang, Fangzhou Hong, Quan Wang, Chai Kiat Yeo, Ziwei Liu, and Chen Change Loy. 2023. Deformtoon3d: Deformable neural radiance fields for 3d toonification. In Proceedings of the IEEE/CVF International Conference on Computer Vision. 9144–9154.
Richard Zhang, Phillip Isola, Alexei A Efros, Eli Shechtman, and Oliver Wang. 2018. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In CVPR.
Zeliang Zhang, Mingqian Feng, Zhiheng Li, and Chenliang Xu. 2024. Discover and mitigate multiple biased subgroups in image classifiers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 10906–10915.
Yufeng Zheng, Victoria Fernández Abrevaya, Marcel C Bühler, Xu Chen, Michael J Black, and Otmar Hilliges. 2022. Im avatar: Implicit morphable head avatars from videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 13545–13555.
Yufeng Zheng, Wang Yifan, Gordon Wetzstein, Michael J Black, and Otmar Hilliges. 2023. Pointavatar: Deformable point-based head avatars from videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 21057–21067.
Wojciech Zielonka, Timo Bolkart, and Justus Thies. 2022. Towards metrical reconstruction of human faces. In European Conference on Computer Vision. Springer, 250–269.
Wojciech Zielonka, Timo Bolkart, and Justus Thies. 2023. Instant volumetric head avatars. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 4574–4584.

Footnote

^⁎Work done during an internship at Adobe Research

Authors' Contact Information: Luchuan Song, University of Rochester, Rochester, New York, USA and Adobe Research, San Jose, California, USA, lsong11@ur.rochester.edu; Yang Zhou, Adobe Research, San Jose, California, USA, yazhou@adobe.com; Zhan Xu, Adobe Research, San Jose, California, USA, zhaxu@adobe.com; Yi Zhou, Adobe Research, San Jose, California, USA, yizho@adobe.com; Deepali Aneja, Adobe Research, San Jose, California, USA, aneja@adobe.com; Chenliang Xu, University of Rochester, Rochester, New York, USA, chenliang.xu@rochester.edu.

CC-BY license image
This work is licensed under a Creative Commons Attribution 4.0 International License.

SIGGRAPH Conference Papers '25, Vancouver, BC, Canada